Bioinformatics: Computing for Molecular Biology

Compression of Molecular Sequences.

The complexity (information content, entropy, compressibility, ...) of DNA and other biological sequences is of interest for a variety of reasons: Repetitive subsequences (poly-A, (AT)^*, etc.) have low information content; they may be of interest in their own right or may be given a low weighting in sequence matches if they can be identified. Informally, two extreme kinds of sequence are "boring", those with near zero information content, e.g. AAAAAAA...., and those with maximum information content, i.e. random sequences, as "typed" by the proverbial monkey. Generally, interesting sequences have some structure or pattern and lie somewhere between these extremes. The Alu sequences form a family of sequences, each about 300 bases long, that occur thousands of time in human DNA. The typical Alu is about 87% similar to the concensus Alu therefore the information content of an Alu is much less than 600 bits. Gene duplication, regulatory signals, codon bias, etc. all reduce the information content below 2 bits/base and may be of biological interest.

• [Example (click)]

• D.R. Powell, D.L. Dowe, L. Allison and T.I. Dix. Discovering Simple DNA Sequences by Compression. Pacific Symposium on Biocomputing 3 (PSB98), pp.595-606, 1998.

• L. Allison, T. Edgoose & T. I. Dix, Compression of Strings with Approximate Repeats, Intelligent Systems in Molecular Biology (ISMB'98), pp.8-16, Montreal, 28 June - 1 July 1998, [HTML] [pdf].
  AED's Approximate Repeats Model (ARM) for DNA sequences allows for approximate forward and reverse-complementary repeats and achieves good sensitivity at pattern discovery.

• L. Allison, L. Stern, T. Edgoose & T. I. Dix. Sequence Complexity for Biological Sequence Analysis. Computers and Chemistry 24(1), pp.43-55, Jan' 2000.

• L. Stern, L. Allison, R. L. Coppel, & T. I. Dix. Discovering Patterns in Plasmodium falciparum Genomic DNA. Molecular and Biochemical Parasitology, 118(2), pp.175-186, Dec' 2001.

• Minh Duc Cao, Trevor I. Dix, Lloyd Allison & Chris Mears.   A Simple Statistical Algorithm for Biological Sequence Compression. IEEE Data Compression Conference (DCC), 2007.
  The expert model (XM) gives good compression of DNA and also protein sequences, and it is fast.

• T. I. Dix, D. R. Powell, L. Allison, J. Bernal, S. Jaeger & L. Stern. Comparative Analysis of Long DNA Sequences by Per Element Information Content Using Different Contexts. BMC Bioinformatics, 8(Suppl.2):S10, May 2007. Information-content plots are compact and show what new information a given context tells about a sequence, and where.

See also the alignment of compressible sequences [below], Comp. Jrnl (1999), etc..

Alignment of Two Strings.

• Personal publications on sequence alignment algorithms.

• TR90/148 Inductive Inference over Macro-Molecules (HTML) (or postscript)

• Source code for 1, 3 and 5-state alignment, both optimal alignment and r-theory.

• Dynamic Programming Algorithms for Sequence Alignment.

One of the products of this work is the alignment density plot (right). This is a good way to visualize the collection of all possible alignments of two strings and the grey-scale level indicates the degree of (un)certainty as to which is the correct or "true" alignment.

The plot from the sequence alignment algorithm shows the degree of certainty and uncertainty in various sequence alignments, see:

• L. Allison, C. S. Wallace & C. N. Yee. When is a String Like a String? Artificial Intelligence in Mathematics (AIM), Ft. Lauderdale, Florida, January 1990 [HTML].

• L.Allison, C.S.Wallace & C.N.Yee. Inductive Inference over Macro-Molecules, Technical Report 90/148 [HTML] or....

• L.Allison, C.S.Wallace & C.N.Yee, Finite-State Models in the Alignment of Macro-Molecules, J.Molec.Evol. 35(1) 77-89, 1992.

• C. N. Yee & L. Allison. Reconstruction of Strings Past, Comp. Appl. in BioSciences (CABIOS) 9(1) pp.1-7, 1993, [HTML].
  By summing the probability over all alignments even very distant relationships can be detected. By averaging parameter estimates over all alignments, rather than just the optimal alignment, unbiased estimates of parameter values are obtained. This is demonstrated for the 1-state (simple) and 3-state (linear, affine gap costs) models.

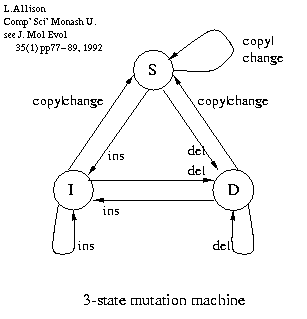The 1, 3 and 5-state (etc.) models are models of alignment, evolution or mutation having increasing complexity.

3-state mutation machine (right) from the MML computational biology sequence alignment program corresponds to affine or linear gap costs as commonly used in aligning DNA sequences, see:

• L.Allison, Normalization of Affine Gap Costs Used in Optimal Sequence Alignment, J.Theor.Biol. 161 263-269, 1993 [www inc' pdf paper].
  You can interpret your favourite integer penalties or scores as probabilities or you can choose integer penalties (scores) that approximate probabilities that you believe are appropriate.

Low- (or moderate-) information content (non-random, repetitive, compressible,...) sequences cause problems in alignment algorithms and in database searching, causing false-positive matches, for example. The information content of the sequences can be taken into account giving better results; see:

• D. R. Powell, L. Allison, T. I. Dix and D. L. Dowe. Alignment of low information sequences. Proceedings of the Fourth Australasian Theory Symposium [CATS98] pp.215-229, February 1998.

• L. Allison. Information-Theoretic Sequence Alignment (HTML), TR98/14 School of Comp. Sci. & SWE, Monash University, June 1998, - on the alignment of non-random (compressible, repetitive, low-information content) sequences.

• L. Allison, D. Powell & T. I. Dix. Compression and Approximate Matching, Computer Journal, 42(1), pp.1-10, 1999 [www inc' pdf paper].

• L. Allison, D. Powell and T. I. Dix. Modelling Is More Versatile Than Shuffling. [TR 2000/98] (HTML), 2000.
  Fewer false positives, fewer false negatives, can (and should) change rank-order of alignments, applicable to more general models than the "shuffling" correction for non-uniform populations of sequences, identifies correct population model(s).

• [Example]

• Seminars: (DNA) Sequence Complexity and Alignment, to the Walter and Eliza Hall (WEHI) Bioinformatics Group, 13 Feb' 2001, on the relationship between sequence alignment, compression & modelling of biological sequences, and alignment of non-random sequences.
  Modelling v. Shuffling, to the Bioinformatics Group & Dept. Computer Science [UWA], 11 Aug' 2004, on PRSS, masking, shuffling, M-alignment, low to medium information content sequences, and alignment accuracy, significance & ranking.

• D. R. Powell, L. Allison, T. I. Dix. Modelling-Alignment for Non-Random Sequences. 17th ACS Australian Joint Conf. on Artificial Intelligence (AI2004), pp.203-214, 6-10 Dec 2004, Springer-Verlag, LNCS/LNAI 3339, isbn:3-540-24059-4.
  Comparison with PRSS from FASTA package. Link leads to software and paper.

• Variations on Sequence Alignment (2007), dynamic programming and related algorithms for two or more sequences.

Minimum message length [MML] is used to compare sequences objectively. MML also gives a natural null-theory and a significance-test for hypotheses. The models are based on finite-state machines (~ hidden Markov models). The theory of multi-state distributions is used to calculate the accuracy of the parameter estimates.

Algorithms.

• L. Allison & T. I. Dix. A bit-string longest common subsequence algorithm, Inf. Proc. Lett. 23(6), pp.305-310, 1986 [paper] [code].
  Uses bit-vector operations to get a speed-up roughly equal to the word-length of the computer.

• L. Allison, Lazy dynamic programming can be eager. Inf. Proc. Lett., 43(4), pp.207-212, Sept' 1992 [paper]
  When written in a lazy functional programming language, the simple, O(n²)-time dynamic programming algorithm (DPA) can be made to run in just O(n.d)-time by adjusting the central comparison test.

• L. Allison. Using Hirschberg's algorithm to generate random alignments. Inf. Proc. Lett., 51 pp.251-255, 1994.
  Allows alignments of two strings to be sampled at random from their posterior probability distribution. This gives a Monte-Carlo method for estimating evolutionary parameters and, when cooled, gives a simulated annealing method for optimal alignment. It has been applied to multiple alignment, see Allison & Wallace Jrnl. Molec. Evol., 39, pp.418-430, 1994 under multiple alignment.

• D. R. Powell, L. Allison & T. I. Dix. A versatile divide and conquer technique for optimal string alignment. Inf. Proc Lett., 70(3), pp.127-139, 1999 [www inc' pdf document]
  Common string alignment algorithms such as the basic dynamic programming algorithm (DPA) and the time efficient Ukkonen algorithm use quadratic space to determine an alignment between two strings. In this paper we present a technique that can be applied to these algorithms to obtain an alignment using only linear space, while having little or no effect on the time complexity. This new technique has several advantages over previous methods for determining alignments in linear space, such as: simplicity, the ability to use essentially the same technique when using different cost functions, and the practical advantage of easily being able to trade available memory for running time.

• L. Allison. Longest biased interval and longest non-negative sum interval. Bioinformatics, 19(10), pp.1294-1295, 1 July 2003.
  Finds the longest interval of a sequence that has at least a specified minimum bias (e.g. 80%) towards certain specified characters (bases, amino acids, e.g. AT). It can process very long sequences quickly.

• L. Allison. Finding approximate palindromes quickly and simply. TR 2004/162, School of Computer Science & Software Eng., Monash U., 2004.

Alignment of Three Strings.

• Fast 3-way alignment procedure: O(n.d²) time at worst, O(n+d³) on average, where the strings' lengths are ~n and d is the 3-way edit-distance.

• L. Allison. A fast algorithm for the optimal alignment of three strings. J. Theor. Biol. 164(2) pp.261-269, 1993 [www inc' pdf paper].
  Simple mutation costs; for affine gap costs see Powell et al 2000

• D. R. Powell, L. Allison & T. I. Dix. Fast, optimal alignment of three sequences using linear gap costs. J. Theor. Biol. 207(3) pp.325-336 Dec 2000 [www inc' pdf paper].
  Gap (indel) costs of the form a+b*k for a gap of length k, where a and b are small integers. The algorithm runs in O(n+d³) time on average, where the string lengths are ~n and d is the 3-way edit distance. i.e. It is fast when the strings are similar, and the edit distance, not string length, is the main influence on running time.

Note that each internal node in an unrooted binary tree has three neighbours so that a good heuristic for k-way alignment, given an evolutionary-tree, is to do repeated 3-way alignment, inferring the strings at internal nodes in the process.

Multiple Alignment and Evolutionary Trees.

• Personal publications in multiple alignment.

• Technical Report 91/155 Minimum Message Length Encoding, Evolutionary Trees and Multiple Alignment.

• L. Allison, C. S. Wallace and C. N. Yee. Minimum message length encoding, evolutionary trees and multiple alignment. Hawaii Int. Conf. Sys. Sci., HICCS-25, v1, pp.663-674, Jan 1992 [paper].

• L.Allison & C. S. Wallace. The Posterior Probability Distribution of Alignments and its Application to Estimation of Evolutionary Trees and Optimisation of Multiple Alignments, Technical Report 93/188, July 1993.

• L. Allison & C. S. Wallace. An Information Measure for the String to String Correction Problem with Applications, 17th Annual Annual Comp. Sci. Conf., ACSC-17, Christchurch, New Zealand, and Australian Computer Science Communications 16(1C), pp.659-668, Jan' 1994 [paper (HTML)]

• L. Allison and C. S. Wallace. The Posterior Probability Distribution of Alignments and its Application to Estimation of Evolutionary Trees and Optimisation of Multiple Alignments. Jrnl. Molec. Evol. 39 pp.418-430, 1994.
  Minimum message length [MML] is used to determine the accuracy with which branch-lengths in an evolutionary tree can be estimated - it is rather low in general. Simulated annealing is used as a way out of the local-optima problem for a practical multiple-alignment algorithm. Gibbs-sampling is used as a practical way of estimating edge lengths, and standard deviations of estimates give another indication of reliable accuracy.

• On Multiple Sequence Alignment

• Source code of a stochastic multiple alignment computer program [6/'95].
  This does iterated, stochastic 3-way alignment at each internal node of the tree to sample ancestral strings. This strategy should be straightforward to adapt to sophisticated mutation models. There is also good potential for speed up on a parallel computer or on a network of workstations.

• Technical Report 95/225 postscript (50K) Towards Modelling Evolution = Mutation modulo Selection in Sequence Alignment.
  Biological evolution takes place through the mutation of DNA modulated by the pressure of selection which determines which changes are viable. A proposal for modelling both of these factors in the multiple-alignment problem is presented. It is argued that tree-based alignment methods primarily model mutations events, and that most non-tree methods (e.g. profiles) model selection pressures on a family of sequences. A tree-based method specifies mutation probabilities and, if used in isolation, the hope must be that biases due to selection are small or average out. A non-tree method can be used to model the family of sequences - which sequences are fit and viable, and which are non-viable, as members of the family. It is suggested that the two approaches can be combined: the latter can be used to modify the mutation probabilities of the former - to model which mutations are viable and are observed.

Restriction Site Mapping.

• Personal publications in mapping.
• L. Allison & C. N. Yee. Restriction Site Mapping is in Separation Theory. CABIOS 4(1), pp.97-101, Jan 1988 (now Jrnl Bioinformatics).

See also Trevor Dix, Darren Platt and C. N. Yee.

Protein Structure.

• Personal publications in protein structure (short).

• Technical Report 92/163 A Decision Graph Explanation of Protein Secondary Structure Prediction. [HTML]

• D. L. Dowe, J. Oliver, T. I. Dix, L. Allison & C. S. Wallace A decision graph explanation of protein secondary structure prediction. 26th Hawaii Int. Conf. Sys. Sci. Vol.1 pp.669-678 Jan' 1993 [HTML]

• D. L. Dowe, L. Allison, T. I. Dix, L. Hunter, C. S. Wallace & T. Edgoose Circular clustering of protein dihedral angles by minimum message length. Pacific Symposium on Biocomputing '96 (PSB96), World Scientific, pp.242-255, Jan' 1996 [paper (ps)]

• T. Edgoose, L. Allison & D. L. Dowe. An MML classification of protein structure that knows about angles and sequence. Pacific Symposium on Biocomputing '98 (PSB98), pp.585-596, Jan' 1998 [paper (pdf)]

Rubik's snake (tm) (right) makes a good digital model for protein folding and is also fun. It is made of 24 triangular prisms which meet on their square faces. Two meeting prisms can rotate relative to each other about the centre of the meeting face so as to vary the "dihedral" angle. The snake can be packed in a ball as a "globular" protein and can form "helices" and "extended" conformations.

Minimum Message Length Encoding.

Many of the above projects make use of a method of inductive inference known as Minimum Message Length [MML] encoding. MML is a realisation of Occam's razor. It is invaluable for dealing with error and uncertainty in data and for comparing models that have different complexities. For example, an alignment-model with gap-penalties is more complex (has more degrees of freedom) than one without gap-penalties. The former will in general fit the data strings better than the latter - but is the improvement enough to "pay for" the extra complexity of the model? MML can judge this trade-off fairly. (Note that maximum-likelihood ignores the complexity of the model which can result in the well known phenomenon of over-fitting.)

Hidden Markov Models

(Hidden) Markov Models (HMM) are often called probabilistic finite state automata (PFSA), or probabilistic finite state machines (PFSM), in computing because of their close relationship to finite state automata, as used in formal language theory. Whatever they are called, they are useful in pattern & structure discovery, compression, alignment of pair of sequences, etc.. [more]

Misc'

Compression and Analysis of Biological Sequences. Why and How [2007], Modelling Alignment, Bioinformatics at CSSE [9/2001], Sequence Complexity.

Researchers

Dr. Lloyd Allison , Dr. Trevor Dix, Prof. C. S. Wallace.