Supporting Notes 3

Some pupils may simply compare the distances calculated. This is false logic. These measurements cannot be meaningfully compared. It is necessary to compare times. The distance measurements are needed for calculating the times.

This is a critical part of the investigation. Teachers need to discuss with students the basic reason WHY the distance calculations are NOT sufficient to make a decision about whether the batsman is IN or OUT. Simply put, the bail and the bat travel at different speeds so comparing the distance travelled by each will not solve the problem. This would be a solution if these objects did travel at the same speed.

In order to calculate the time taken in each case, we must have a reliable estimate of both the speed of the batsman and the speed of the falling bail.

To determine the time that the bat has been over the crease-line, the extra information needed is the speed of the batsman.

To determine the time that the bail has been off, the extra information needed is the formula for a body in free fall

This can be used to calculate the time (t sec) taken for the bail to fall d metres, using the value of d determined from the photograph.

Some teachers may prefer their pupils to collect primary data. This option would need an extra lesson. Using a think-pair-share in their groups, pupils could design an experiment to determine the speed of a batsman sprinting to reach a crease-line. One or two ‘volunteers’ should be timed running the equivalent of the length of a cricket pitch, fully attired as a batsman in a test match. It is expected that pupils would mark out this distance and time a ‘batsman’ over several trials. The class upper and lower limits for speed would be recorded. As part of this discussion, pupils compare the ‘experimental’ speed with their initial estimates.

Teachers may use the video clips supplied. In this case, students will know the distance travelled by the batsman and can time the event from the video clip. Students will need stop watches for this. In trial classes students subtracted one metre from the distance run by the batsman to compensate for ‘backing up’, that is the distance which the batsman has already advanced (walked) down the pitch while the bowler bowls the ball before beginning to sprint in taking the run. Teachers may like to run the video clip at normal speed or at reduced speed in order to increase the accuracy of the calculation. The speed of the clip will be known from the computer package chosen to show the clip. Once again class upper and lower limits are recorded and the data compared with the pupils’ estimates.

An investigation of the frame rates reveals the NTSC TV standard in the 1960 was 29.97 fps. The windows Codec 9 standard for the windows media video files (.wmv) is 25 fps. You should be able to play the videos frame by frame with the knowledge that you are viewing them at 1/25th sec intervals.

Knowing that the average speed of an Olympic athlete is approximately 10 metres per second, speeds calculated from video clips range between 5 and 6 metres per second.

During this discussion, it is likely that students may raise any of a number of factors that might (and in many cases will) affect the speed of the bat, but which involve a more complex model than the one being developed first. These ideas should be affirmed and preferably recorded, to be used in lesson 4, when the initial assumptions are revisited. Teaching and learning issue 3 describes how this became apparent during the trialling.

Teaching and Learning Issue 3: Keeping a brainstorm manageable

This vignette is written in the voice of an observer of the first class where this sequence was trialled; at that time, we had not identified the issue of dealing with the many possible factors in two stages of modelling.

Bill, the teacher, opened up the discussion of how they might determine the speed of the batsman. What was implicit in his thinking, but not explicit in what he said to his pupils, was that initially it was going to be best to assume that the batsman was running at the same speed all the way down the pitch. .Given this assumption, he wanted ideas on ways that the class could get a reasonable estimate of this speed. The class were enthusiastic participants, but immediately raised issues that were outside the model Bill was thinking of.

“We could measure someone out on the oval” and “Yes but they might be slowing down because they get tired” and “He might have made a final sprint when he realised that it was going to be close” and “Suppose he was straightening his arm just as he crossed, that would speed up the bat”

There were a range of other comments. Bill realised that he had a problem; he recognised that all of the comments were genuine and sensible and he recorded and praised each of them as they were made. However he only wanted to use ones like the first one in what was intended to be the next task and he did not want to just dismiss the others. He guided the discussion to the ones that he wanted to use, and I could see some of the students whose ideas seemed to be sidelined become less involved. It was only after the lesson that we thought of being explicit with the students about the issues of modelling and of beginning with a simple model, but recognising the assumptions and later revisiting these. In later trials this provided a way of keeping the initial calculations manageably simple, but not dismissing the students’ creative thinking.

Close Box

The background notes on Factors 5, 6 & 8 are relevant here. The batsman has been assumed to have a constant speed and so the equation connecting distance and time is linear. Falling objects accelerate and so the equation is a quadratic (d = 4.9t²). It is likely that going into any detail of the relevant science will be inappropriate for your pupils and what follows is intended as background for the teacher. If you do decide to discuss this in more detail, then there are two crucial issues. The first is that many pupils do not appreciate that objects accelerate under gravity when dropped; the acceleration is too rapid to perceive and many pupils are likely to believe that, when dislodged, the bails instantaneously gain a (high) constant speed. Instantaneous acceleration would require an infinitely large force and is thus impossible; however this issue is now a long way from the run-out decision!

The second piece of relevant science is that, ignoring air resistance, all objects, regardless of mass, fall with the same acceleration, hence there is a single formula that covers them all. Simultaneously dropping two objects of very different mass will demonstrate this (unless one is so shaped that the effect of air resistance is much greater). A third, even more sophisticated issue is that the downward component of velocity is unaffected by whether or not there is a sideways component –in other words a bail knocked sideways will hit the ground at the same instant as one falling vertically (with a little effort, this can also be demonstrated in class). Note that any initial upward motion will make a difference – the bail has to slow down, stop and then has a greater distance to fall.

Where d is the distance travelled in metres, u is the initial speed in metres per second, a is the acceleration in metres per second per second, and t is the time in seconds.

For an object falling under the influence of gravity, the initial speed u is zero, and the acceleration due to gravity is 9.8 metres per second per second.

(Note: these are not the ‘required’ answers, but an example of results that pupils may determine.)

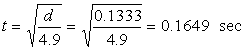
The batsman is OUT because the bail has been off for longer than the batsman has been past the crease-line.