LESSON THREE: A MATTER OF TIME
LESSON THREE: A MATTER OF TIME |
GOALS OF LESSON
This lesson is designed to reinforce to pupils HOW mathematics can help them make the decision about whether the batsman in the photograph is IN or OUT.
In this lesson, pupils will use the factors from lesson two, namely the distance the bail has fallen and the distance the bat has travelled past the crease-line, to calculate the time taken by the bail to fall as well as the time taken for the bat to travel past the crease-line. In this way pupils will be able to decide whether the batsman in the photo was IN or OUT.
FEATURES OF THE LESSON
Pupils think more deeply about the problem in terms of how mathematics may be used to help them make the run-out decision.
Pupils identify the factors which are necessary in order to solve the problem.
Pupils calculate both the time taken for the bat to pass the crease-line and the time taken for the bail to fall.
Pupils make a decision based on these calculations as to whether the batsman is IN or OUT.
Pupils compare their answer with previous estimates and gain a deeper understanding of the very short times involved when an umpire has to make such a decision without the assistance of technology.
SUMMARY
Pupils discuss the homework activity – discuss and get feedback on calculations using the distance-speed-time relationship and the use of scale factor (10-15 minutes). |
¯ |
Pupils estimate the speed of a batsman, and then determine some values using a number of possible techniques (10-15 minutes). |
¯ |
Pupils calculate the time taken for the bat to travel past the crease-line (10 minutes). |
¯ |
Pupils calculate the time taken for the bail to fall (10 minutes). |
¯ |
Pupils use the calculations of time to decide whether the batsman is IN or OUT. This process is part of modelling the system with initially a simple model, but recognising that some simplifying assumptions have been made and these will be explored later (10 minutes). |
PREREQUISITES
Pupils should have completed their homework from lesson 2.
Pupils need to have learned the relationship between distance, speed and time and be able to use it to calculate time.
If students have never substituted data into an equation such asPREPARATION
Pupils will need a copy of the photograph from lesson 1.
Pupils will need rulers and calculators for this lesson. They may also need stop watches.
You will also need to be able to show the video clips again, using a laptop computer and data projector.
Photocopies of Worksheet 3 (optional).
PRIOR LEARNING FOR LESSON THREE
Students should be familiar with the following concepts:
Measurement of distance and time using simple instruments such as rulers and stop-watches;
Scale and how it is used to convert a distance on a picture to a real distance. Pupils may have met this concept in their study of Geography;
Decimal numbers, such as 0.1 and 0.23, being able to rank them from least to greatest and their understanding of place value in this work;
The substitution of numbers for pronumerals into a mathematical formula in order to calculate a result. Pupils may have met this work in formal algebra, or in their study of measurement (formulae for area and volume);
PLAN
3.1 WHOLE-CLASS DISCUSSION – WHAT FURTHER INFORMATION DO WE NEED?
A good way to begin the lesson would be by reviewing pupils’ answers to the previous night’s homework. If pupils did not complete lesson 2 homework then you will probably need to allow time for these questions to be done now. Pupils should be confident in their ability to use the speed-time-distance relationship to undertake simple calculations, as well as the use of scale factor in simple problems.
Now ask pupils to consider how the distances calculated in lesson 2, together with the speed of the batsman, can assist with solving the problem. What else do we need?
Ascertain whether pupils have managed to think beyond the calculation of the distances from the previous lesson and have seen the need for a calculation of the TIMES of both the bail to fall and the bat to travel past the crease-line. In order to calculate these times, we must have an idea of the SPEED of each object. (Advice for Teachers #3.1)
3.2 CALCULATION OF THE SPEED OF THE BATSMAN
The aim is for pupils to gain a reliable estimate of the speed of a test batsman.
Pose the question:
Do you think all batsmen run at the same speed?
How fast do batsmen run when they are fully kitted out with pads, protector, gloves and bat?
In pairs, ask pupils to come up with an estimate of the speed of a batsman, providing some justification. (For example, they could consider whether the batsman is likely to be running faster or slower than a champion athlete in the 100 m sprint event at the Olympics.)
They then decide how to calculate an estimate of the speed, either by obtaining primary data from a fully equipped batsman (Advice for Teachers#3.2), or by using a video-clip (Advice for Teachers #3.3). Instructions for showing video clips are supplied and are also relevant to lesson 1. It is important, during this discussion, that the pupils are aware that, as a first stage of making a decision, they are going to model the situation in the simplest way. (Advice for teachers#3.4),
Teaching and Learning Issue 3: Keeping a brainstorm Manageable
3.3 CALCULATION OF THE TIME TAKEN FOR THE BAT TO TRAVEL PAST THE CREASE-LINE
Pupils should use their findings for the speed of the batsman to calculate the time the bat has travelled beyond the crease-line, having first measured the distance the bat has travelled beyond the crease-line from the photograph.
They will need to use the formula time = distance / speed.
3.4 CALCULATION OF THE TIME TAKEN FOR THE BAIL TO FALL
Choosing one bail, pupils should estimate how long they think it took to fall to its current position shown in the photograph. This reveals the problems of trying to measure this empirically and that a formula will be needed. In a way that is appropriate to the class level, bring out the issue that the motion of the bail is different to the motion of the batsman and so requires a different formula. This area in one where it may be appropriate to make links to relevant science content. (Advice for teachers #3.5)
Introduce the formula for a body in free fall to calculate the time (t sec) taken for the bail to fall d metres, 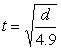 .
.
Use the value of d determined from the photograph. Pupils need to assume that the bails fall straight down from the top of the stumps.
(The derivation of this formula is beyond pupils at this level, but might be of interest to advanced pupils.)
It may be appropriate to hold a brief discussion of accelerated motion, but be careful not to delve too deeply into this concept. However, there does need to be an introduction to the concept that the motion of the bail is different to the motion of the batsman. All objects fall at the same acceleration whereas all batsmen run at different speeds. Pupils can collect primary data for the speed of the batsman but it is very difficult to collect primary data on the falling bail. You could try this - pupils will soon realise that the time is too short to measure and that therefore they need to rely on the formula given to be able to determine the time the bail has been falling.
Pupils will need reassurance that the times which emerge from these calculations are SMALL numbers, of the order of one or two tenths of a second. This is to be expected. World records in events such as the 100 metre sprint are decided by tenths, hundredths or even thousandths of a second, and often in sport such short times mean the difference between winning and losing. You can now sympathise with the umpire in a county game of cricket who only has this very short amount of time to make this judgement by eye. The human eye can distinguish between one and two tenths of a second, but events which involve time differences of a few hundredths of a second cannot be judged by the human eye. Hence the need for technology!
3.5 ACTIVITY – PUTTING IT ALL TOGETHER
Pupils should compare their calculations for the time taken by the bail to fall with the time taken by the bat to travel beyond the crease-line, and then review their response to the key question: Was the batsman IN or OUT?
Teachers should refer to the sample calculations provided as a guide to facilitating this work with pupils.
If the batsman’s bat has been past the crease-line for 0.20 seconds, and one bail has been off the stump for 0.15 seconds, is the batsman IN or OUT? Give a clear explanation showing your reasoning.
If the batsman’s bat has been past the crease-line for 0.22 seconds, and one bail has been off the stump for 0.27 seconds, is the batsman IN or OUT? Give a clear explanation showing your reasoning.
What’s your decision - was the batsman was IN or OUT?
Write a clear argument for your decision using all the data and facts discovered and/or calculated in the lessons.
In your calculations you have made several assumptions. For example, one such assumption is that the batsman ran in a straight line.
Write a list of any other assumptions which may have had an effect on your calculations.
.