Supporting Notes 2

Each of these measurements is critical. Each has a direct bearing on whether a batsman will be IN or OUT. These are measurements for which it is possible to make estimates and measurements from the photograph.

It is not possible to measure this from the still photograph, but it is a critically important factor. The speed of the batsman is related to two other critical variables: the distance of the bat-tip past the crease-line and the time that the bat-tip has been past the crease-line.

This factor is related to factors 2 and 3. The significance of this factor should emerge by the end of Lesson 3. Using an estimated running speed of the batsman and the indirectly measured distance that the bat-tip is past the crease-line, pupils will be able to calculate a value for this factor.

This factor is related to factor 1. The significance of this factor should emerge by the end of Lesson 3. Using the formula for the distance an object falls under gravity, and the indirectly measured distance that the bail has fallen, pupils will be able to calculate a value for this factor.

The weight of the bail does not affect the time it has been falling. Teachers could demonstrate this by dropping a ball and a bail (or two objects of with obviously different mass) from the same height. Note: very light objects such as feathers are affected by air resistance, and would be best avoided in such a demonstration.

The weight of cricket bats does vary slightly and this would have a small impact on the running speed of different batsmen, but it is not a factor that is useful to investigate in this situation because the effect on the result would be insignificant.

The issue of whether the bails fall straight down off the stumps is important and does have a bearing on the result. Sometimes the bail does not fall straight off the top of the stump to the ground. Bails can fall in a variety of trajectories – some of which include initially moving up. However, the physics of this is beyond pupils at this stage. To simplify later calculations of time and distance, it is recommended that pupils are told to assume that the bails fall straight down. The implications of this assumption must then be addressed in Lesson 3, Lesson 4, and Lesson 5 as part of the discussion of the role of assumptions in modelling.

In trials it was found that pupils were convinced of the significance of the position of the ball. This might arise from pupils’ understanding that it is the inter-play of the bat, ball, and bails that determines whether the batsman is IN or OUT. However, pupils need to realize that the ball has done its work once we see the photograph. Determining the current position of the ball is not relevant.

It is the speed that the batsman is running when the bat goes over the crease-line that is important. To simplify the model, pupils will need to estimate and use a measure of the average speed of the batsman.

Pupils may argue that the distance and time that the batsman has been running are important. Some pupils also identify the acceleration of the batsman as important (acceleration discussion). These considerations are not irrelevant, but they are not factors that can be measured in the situation. Focus pupils on the need to consider the instant that is captured in the photograph.

In trials this emerged as a factor of importance to some students, particularly when viewing video clips of run-outs. This method of judging whether a batsman is IN or OUT is based on someone already having made an IN or OUT decision. It is not a factor that can be quantified.

The challenge for teachers is to allow this understanding to emerge from the discussion. Read the Background notes on factors in making the run-out decision but avoid directing the discussion by reading these out to pupils or giving them this information in some other form.

Try to let pupils arrive at the understanding of what factors are critical by repeatedly posing questions like:

In trials, a useful technique was found to be writing the list on the board and having pupils agree together which could be eliminated. Those that are left can be ranked in order or priority.

The run-out situation is actually a very complex system in which the times of two moving objects are being compared. Therefore, in order to quantify the situation, the system must be simplified.

Since it is likely that most pupils will have had little prior experience with the process of developing a mathematical model, it is reasonable to expect that they may need some guidance to help them develop the understanding of which factors are relevant and can feasibly be investigated.

In Lesson 1 pupils are invited to think of as many factors as they can which might influence whether the batsman is IN or OUT. As well as naming the critical factors, they are likely to throw in many ideas which are either loosely connected or irrelevant.

In Lesson 2 the model is simplified by reducing the list to two factors. Some ideas need to be set to one side (after pupils are convinced of the reasons for doing so), and others (the speed of the batsman) will be re-introduced later.

In Lesson 3 some complexity is built back into the model through the investigation of the speed of the batsman.

In Lesson 4 further complexity is introduced by having pupils investigate the validity of the assumptions they have made in developing their model.

The issue of which units to use should be decided within the groups. Making this decision is part of the process of quantifying the situation. The system of units chosen for the distance measures will need to match that chosen for the running speed, later on. In trials, some pupils made an error here but this was corrected within the groups or following whole class discussions.

Pupils may or may not think about the necessity of calculating two scale factors due to the perspective issue. If they apply the vertical scale factor (for the bail distance) to calculate the distance of the bat tip past the crease line, then they will make an error. The bat is in a plane that is oblique to the stumps. Do not correct pupils if you notice this occurring. It would be preferable to let this issue arise in the whole class discussion.

Teaching and Learning Issue 2: The need for hands on experience

One of the trial teachers commented on how he needed to rethink his instinctive practice of anticipating or immediately fixing problems that arose.

A mathematics teacher’s role includes ensuring that, having learnt a body of knowledge the pupil is able to use this to calculate the correct solution to a question. After running the recent series of lessons, I found myself being challenged on this second point. Is getting the answer right the most important factor in a mathematics teacher’s job?

There’s a lot to be said for stepping back and letting the pupils solve a problem on their own. I think in mathematics it is against our nature to stand and watch a group of pupils making mistakes and struggling to understand a concept or idea. We can find ourselves providing guidance too quickly and thus taking away the window of opportunity that existed, for a pupil or group of pupils to discover the answer themselves.

I was not the only one to struggle with the concept of allowing the pupils time to struggle with the problem in hand, my teaching assistant was evidently stressed and seemed annoyed that I wasn’t ‘helping’ the students. Was it not more important that the students had the chance to solve a puzzle and get stuck and frustrated whilst searching for a breakthrough? I decided, against the appeals of the teaching assistant, to allow the students the chance to solve the puzzle in their groups. It was time to step back.

It was evident from the plenary and evaluation stages of the lesson that the majority of the pupils had tussled with the calculations and that some had failed to complete all the solutions. So was I to determine this stage of the cycle a failure? I would suggest not. Upon reflection I would have changed a number of questions slightly, but this would have been purely to lower the level of the mathematics slightly. Would I change the way I had supported the pupils in the lesson? No. I had facilitated learning, rather than lead it. By stepping back, I had given the pupils the opportunity of making mistakes, but then also I had given them the chance to discuss the problem amongst themselves so that they could correct they mistakes and solve the problem without my input. This is an important skill for our pupils to learn.

Close Box

In trials pupils came up with a variety of answers which gave teachers the opportunity to state that “different answers were acceptable”. One teacher urged some pupils “not to cross out your answers” which they started to do when they heard other pupils giving values that differed to theirs.

The fact that there is a range of answers can be used to highlight the fact that all measurements are approximations. The error that is introduced is one of number of factors that introduce doubt into the final decision. In Lesson 4 and Lesson 5, pupils consider their original decision in the light of ‘reasonable doubt’.

Some pupils may simply compare the distances calculated. This is false logic because the objects are not travelling at the same speed. These measurements cannot be meaningfully compared. It is necessary to compare times. The distance measurements are needed to for calculating the times*.

*Allow this understanding to develop from the discussion at the beginning of lesson 3.

To determine the time that the bat has been over the crease-line the extra information needed is the speed of the batsman.

To determine the time that the bail has been off the extra information needed is the formula for a body in free fall .

This can be used to calculate the time (t sec) taken for the bail to fall d metres, using the value of d determined from the photograph.

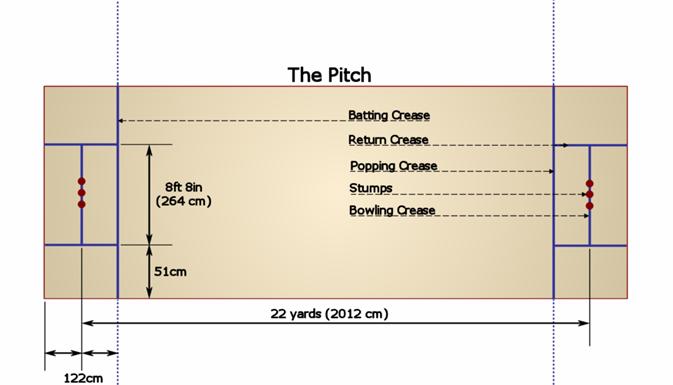
In order to obtain more reliable estimates for each, pupils will need to use the standard measurements of crease-lines, bats and stump height.

(Note: these are not the ‘required’ answers, but an example of results that pupils may determine.)

Scale factor for stumps: 32 : 711 = 1 : 22.22 (This will vary according to the reduction of photo.)

On the photograph the bail has fallen = 6 mm (lowest bail is first one knocked off. Measurement made at the centre of the bail.

* note: this measurement will vary according to the printer and/or photocopier used.

(*Note that due to perspective the distance between the crease lines varies depending where you make the measurement. This means pupils need to make a decision about where this measurement should be made. In this calculation, the distance was measured along an imaginary line on which the bat tip lies. This line is parallel to the side edge of the crease. You might choose to discuss this with your pupils at this point or leave this until the discussions on assumptions which should take place in later lessons.)

b. You would need to convert the time unit from hours to seconds. (2 hours = 120 seconds)

b. You would need to either convert the distance unit from kilometers to miles, or convert the speed unit from miles per hour to kilometers per hour.