FP II Ver'1.1 Iris #unsup. #better #sup. |
Unsupervised classification
Unsupervised classification (clustering, mixture modelling) of Fisher's (Anderson's) Iris data.
The data type Flower literally defines the type of the data-set,
module Main where
import StatisticalModels
type SepalLength = Double -- @0, defining the attributes
type SepalWidth = Double -- @1
type PetalLength = Double -- @2
type PetalWidth = Double -- @3
-- a datum is a 4-tuple (+ species name)
type Flower = (SepalLength, SepalWidth, PetalLength, PetalWidth, String)
dataAcc = 0.1 -- data measurement accuracy
variate4 m0 m1 m2 m3 = -- 4 x model -> 4-variate model, (m0, m1, m2, m3)
let nlP (d0,d1,d2,d3) =
nlPr m0 d0 + nlPr m1 d1 + nlPr m2 d2 + nlPr m3 d3
in MnlPr (msg1 m0 + msg1 m1 + msg1 m2 + msg1 m3)
nlP
(\() -> "[v4 " ++ show [m0,m1,m2,m3] ++ "]")
estVariate4Weighted e0 e1 e2 e3 ds ws = -- 4 x estimator -> estimator4
let (d0s, d1s, d2s, d3s) = unzip4 ds
in variate4 (e0 d0s ws) (e1 d1s ws) (e2 d2s ws) (e3 d3s ws)
-- NB weighted for mixture modelling
estimator4 = estVariate4Weighted -- our estimator
(estNormalWeighted 0 10 0.1 5 dataAcc)
(estNormalWeighted 0 10 0.1 5 dataAcc)
(estNormalWeighted 0 10 0.1 5 dataAcc)
(estNormalWeighted 0 10 0.1 5 dataAcc) -- i.e. 4 indep. attributes
-- ------------------------------------------LA--24--Nov--2004--CS--Uni--York--
analyse est dataSet n = -- 1..n classes
let
nlys m =
if m > n then putStrLn( "--")
else
let mx = estMixture (take m (repeat est)) dataSet
in putStrLn( show m ++ ": " ++ show mx )
>> putStrLn( "message = "
++ show(msgBase 2 mx dataSet ) ++ " = " ++ show(msg1Base 2 mx)
++ " + " ++ show(msg2Base 2 mx dataSet) ++ " bits" )
>> nlys (m+1)
in nlys 1
main = print topline
>> putStrLn "-- Fisher's / Anderson's Iris data --"
>> readFile "data/iris.data" -- connect data file
>>= \str ->
let flowers = read str :: [Flower] -- read input
(d0s, d1s, d2s, d3s, d4s) = unzip5 flowers
dataSet = zip4 d0s d1s d2s d3s -- NB. discard species
in
>> analyse estimator4 dataSet 4 -- model @0...@3
>> putStrLn "-- finish --"
-- ----------------------------------------------------------------------------
|
| 24 Nov 2004, C.Sci., U.York |
| [data/iris.data] |
#classes message length (bits) 1 3113.8 2 2648.8 3 2573.6 4 2551.4 C.Sci., U.York, 24/11/2004 - There are actually 3 species (the unsupervised classification algorithm is not told that), Iris-setosa (IS), Iris-versicolor (IVe), and Iris-virginica (IVi):
- @0 @1 @2 @3 Iris setosa N(5.0,0.35) N(3.42,0.38) N(1.46,0.17) N(0.24,0.11) Iris versicolor N(5.94,0.52) N(2.77,0.31) N(4.26,0.47) N(1.33,0.20) Iris virginica N(6.59,0.64) N(2.97,0.32) N(5.55,0.55) N(2.03,0.27) - IVe and IVi obviously overlap a great deal on @0, @1 and @2, and IS has notably smaller values than IVe & IVi for @2 and @3.
- IVe and IVi obviously overlap a great deal on @0, @1 and @2, and IS has notably smaller values than IVe & IVi for @2 and @3.
- The slightly lower message length for
4 classes may be due to correlation between the4 attributes (which could perhaps be "accounted for" by a suitable model).
A Better Model
- A custom model and estimator were created to address correlations between "size" attributes.
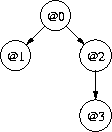
- that is <@0, @1|@0, @2|@0, @3|@2>
(also see [Bayesian nets])
Note the use of the normal distribution for @0 and of the linear regression for @1|@0, @2|@0 and @3|@2 above.custom4Model m0 fm1 fm2 fm3 = -- @0 let nlP (d0,d1,d2,d3) = -- / \ nlPr m0 d0 + condNlPr fm1 d0 d1 -- @1 @2 + condNlPr fm2 d0 d2 + condNlPr fm3 d2 d3 -- \ in MnlPr (msg1 m0 + msg1 fm1 + msg1 fm2 + msg1 fm3) -- @3 nlP ...and a show method... estCustom4Weighted e0 e1 e2 e3 ds ws = ... custom4 = estCustom4Weighted (estNormalWeighted 0 10 0.1 5 dataAcc) -- @0 (estLinear1Weighted (-5) 5 0.1 5 dataAcc) -- @1|@0 (estLinear1Weighted (-5) 5 0.1 5 dataAcc) -- @2|@0 (estLinear1Weighted (-5) 5 0.1 5 dataAcc) -- @3|@2 main = ... >> analyse custom4 dataSet 4 -- cluster with the new model- This model gave lower message lengths all round:
-
#classes message length (bits) 1 2898.8 2 2447.7 = 123.2+2324.5 3 2450.0 4 2450.2 11/11/2005 - A two-class mixture is best;
the three- and four-class mixtures were degenerate with
the extra classes evaporating.
When the "secret knowledge" of the three species and their memberships
was used to create a "true" three-class mixture with this estimator,
it gave a two-part message length of
2452.0 bits (= 173.3 + 2278.6), which is4.3 bits worse than the 2-class mixture found without this knowledge. The 2nd-part, data|model, is better for three species v. two classes but the worse two-part total suggests that the the more complex "true" model would be a case of overfitting for the limited information given to the mixture modeller. Could a botanist confidently infer the existence of three species given only the four measurements from just 150 specimens?- Fisher 1936: "... I.setosa is a "diploid" species with 38 chromosomes, I.virginica is a "tetraploid" with 70, and I.versicolor ... is hexaploid. [Randolph suggested that IVe] is a polyploid hybrid of the two other
species. ..." Note that the present data does not include this information. - Fisher 1936: "... I.setosa is a "diploid" species with 38 chromosomes, I.virginica is a "tetraploid" with 70, and I.versicolor ... is hexaploid. [Randolph suggested that IVe] is a polyploid hybrid of the two other
Supervised Classification
Fisher used the Iris data for a case study in supervised classification; this is completely different from unsupervised classification. A classification-tree is one tool that can be used for supervised classification: From training-data, learn a function-model so that when given measurements from a new flower you can predict which species it most likely belongs to.
data Species = IS | IVe | IVi deriving (Bounded, Enum, Eq, Show) string2Species "Iris-setosa" = IS string2Species "Iris-versicolor" = IVe string2Species "Iris-virginica" = IVi op = map string2Species d4s -- i.e. strings -> Species ct = estCTree estMultiState splits dataSet op |
- The program yields this tree:
{CTfork @3<|>=1.0[ {CTleaf mState[0.98, 0.01, 0.01]}, {CTfork @3<|>=1.8[ {CTleaf mState[0.01, 0.89, 0.10]}, {CTleaf mState[0.01, 0.03, 0.96]} ]} ]}- tree : 62.7 = 28.7 + 34.0 bits
- null : 237.7 = 150 * log2(3) bits
- tree : 62.7 = 28.7 + 34.0 bits
- Recall that only the predicted variable, here Species, is compressed in supervised classification.
Notes
- As given, the data happen to be grouped -- first IS then IVe then IVi.
This is how Fisher presented it.
Unsupervised classification makes no assumption of similarity between data that
are near each other in the data-set;
it should give the same answer if the data-set is randomly permuted.
But if it is appropriate to make such an assumption,
that proximity implies similarity, then
you have a [segmentation problem].
- Search the [bib'] for
[Fisher Iris c193x] .- The data set is available at the UCI machine-learning repository (2004).
|