Strain Incompatibility and Simple Shearing: Implications for Gold and Granite Emplacement |
| Copyright 2005-2009 by Roberto Weinberg. All rights reserved. Unlimited permission to copy or use is hereby granted for non-profit driven enterprise subject to inclusion of this copyright notice and my World Wide Web URL: users.monash.edu.au/~weinberg. We would very much appreciate an email stating how this material will be used. Thanks, RW. |
Fluid pumping and shear zones
The model geometry (A)
corresponds to a horizontal crustal section
undergoing internal simple shear and bounded north and south by
vertical (into the page) sinistral shear zones. Shearing is applied at
right angles to a north-south lithological contact, and two triple
points are defined where this contact intersects the shear zone. Each
block has different physical properties corresponding to different
lithologies, which are modeled as elasto-plastic (Mohr-Coulomb)
materials. We wish to investigate how changes in the elasto-plastic
parameters control deformation, mean pressure and volume strain
distribution.
The asymmetry of simple shear deformation, leads to important
differences in the mechanics of the upper and the lower triple points.
While the upper triple point accommodates the movement of the stronger,
high shear modulus layer towards the weaker layer, the lower triple
point accommodates the movement of the weaker layer towards the
stronger. This asymmetry will lead to important differences in the
nature of deformation between the two.
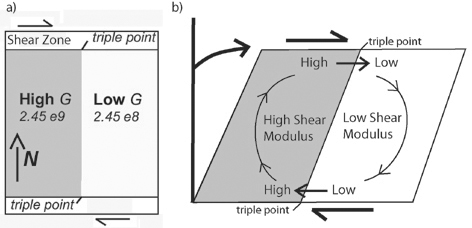
Figure 1. Elastic Model. Volumetric Strain Increment (VSI) for a purely elastic model used to undestand the nature of the elastic response. While the weaker (lower shear modulus) right-hand-side show little variation in strain increment, the stronger (left-hand-side) shows wide variations, from positive values (volume increase) on its upper side, to negative values (volume decrease) on its lower side. In this case, fluid will migrate from the shear zone into the area of volume increase on its shoulder(left).
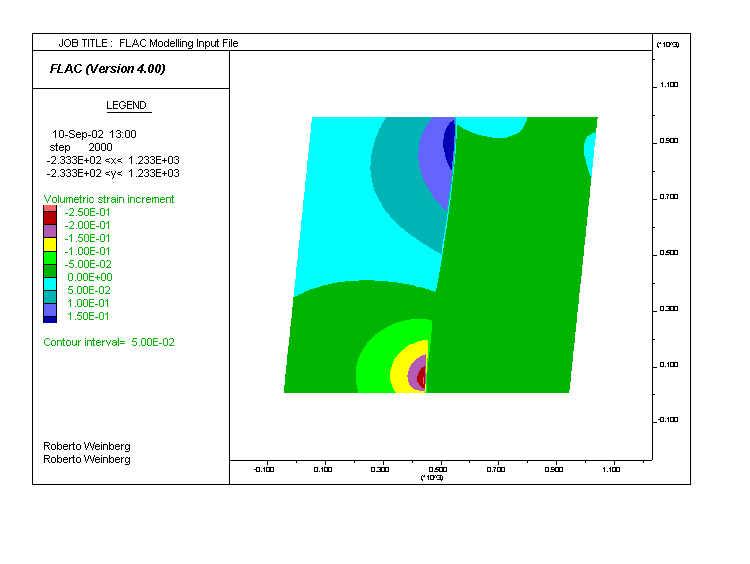 |
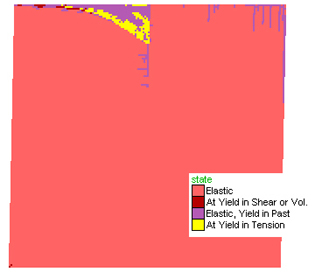
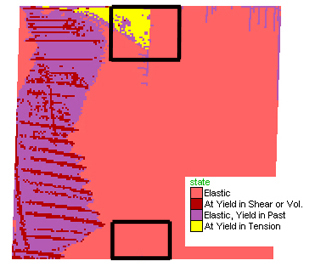
Figure 2. Dextral shearing of a horizontal plane at the Earth's surface (Figure 5 shows results of shearing at a depth equivalent to 2 kb). Three images depicting the state of the evolution of shearing of the initial model block. In the earliest stage (left) a wedge-shaped zone of tensile yielding (yellow) develops at the upper triple point between the two layers and the shear zone. As deformation progresses (middle and right-hand-side figures) a conjugate pair of shear planes develop (red), one of which is parallel to the shear direction and the other at high angles. As deformation progresses shearing along these planes tend to dominate the brittle deformation. Boxes in the middle figure represent indicate the positions of diagrams in Figure 4.
 |
 |
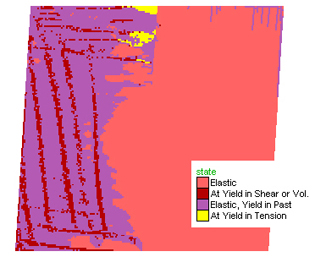 |
Figure 3. Maximum stress axis vectors at a small area close to the triple point on the middle figure above. The orientation of the maximum stress axis is indicative of the most likely orientation of any tensile cracks that develop allowing the development of quartz veins or magma dykes. Note the significant decrease in size of the vectors on the weaker layer to the right.
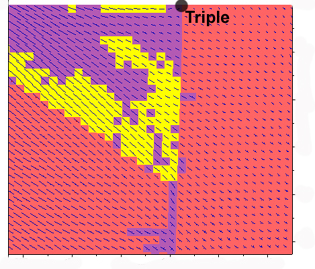
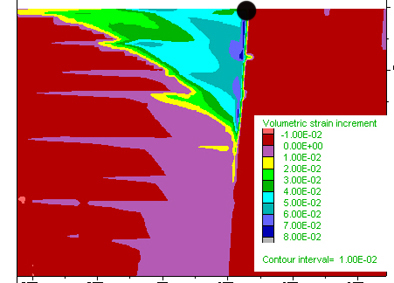
Figure 4 A) Volume Strain Increment (VSI) throughout the entire wedge close to the upper triple point. Positive values indicate volume increase during tensile cracking. B) VSI for the opposite (lower) tripple point where negative VSI implies volume decrease. Black dots represent the triple points.
 |
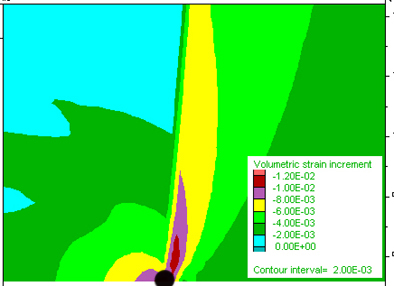 |
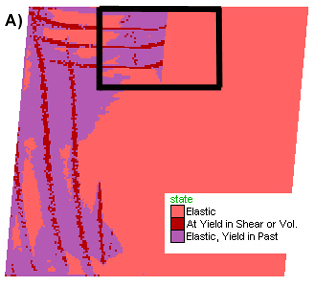
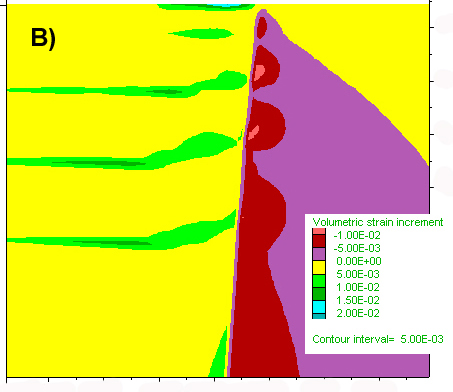
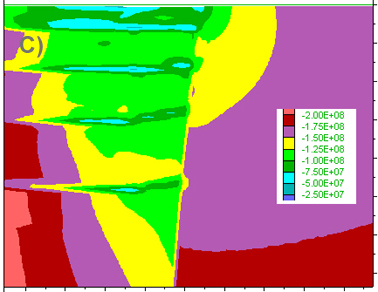
Figure 5. Results of a calculation similar to that of Figs 2-4, but at a depth equivalent to 2kb. A) Red lines depicts regions which are at yield in shear, indicating the likely development of a pair of conjugate shear zones. No tension gashes are likely to develop in the absence of fluid pressure. B) Depicts a detail of the volume strain increment plot, close to the triple point (see box on A) and shows that dilation occurs within the strongest block (left), while the weakest rock looses volume. Similar results were found for runs deeper in the crust, the main difference being that yielding in shear first takes place after larger strain accumulation. C) Detail of A) (box at triple point) showing the reduction in mean pressure along the shear zones (blue colours are low values, red and purple are high). Like at shallower levels, magmas or fluids rising within the shear zone will tend to migrate into the dilational zone close to this triple point. In these calculations, in the absence of fluids, no tension cracks develop. In the presence of fluids, a gradual increase in differential stress, when deformation is initiated, may lead to the development of such cracks.
|
|
 |
These simple models illustrate the role of different shear moduli in controling deformation across a contact during simple shearing. Dilation will take place within a wedge within the stronger rock, when the sense of shear is symmpathetic with most likely to lead to tension cracks curving away from the shear zone and parallel to the axis of maximum compression where quartz veins and magmas will tend to be emplaced. When the