FP II Ver'1.1 ≥1 seq .2-seqs ..t's'm' .dpa ..dpa c2m ..& states .app'-rpts ..edits ..t's'm .Classes .Refs. |
This is a case study of
| Note that TimeSeries provide the simplest case where a data-set itself, cf. a datum in the set, has structure, i.e. sequentiality. (Unless one considers series = datum.) |
Part (i) was not too difficult using class TimeSeries and type TimeSeriesType from [200309] provided that context2model :: tsm ds -> [ds] -> model ds was added to the class. The DPA was general and quite simple; it was able to remain "unaware" of the details of the given time-series model, except for whatever length of recent history "made a difference" in the local incremental choice of an optimal alignment. But it was soon realised that stateful time-series models would require a slightly different version of the algorithm because they cannot be efficiently "paused and restarted" on an arbitrary context::[ds]. This was a nuisance and there would be trouble using context-based and state-based models together.
A new problem appeared over the approximate-repeats model[4]; this requires a sub-model over Jump destinations which almost always depends on the current position within the string being generated. At first it was thought that the length of the context would be useful. This takes O(n)-time to calculate on demand, but could be pre-calculated by the class machinery. There again, some future model would likely need some other property of the context, so where would it end? In any case, the length was not sufficient; the present model needed the number of characters generated or scanned which is ≤ the context length. It seems that the approximate-repeats time-series model requires stateful models -- for efficient implementation.
After further experiment
it appears that while class TimeSeries
(with predictors but without context2model)
is a super-class of class TimeSeriesS
The 2-D DPA was "easily" converted to use TimeSeriesS models. The algorithm became simpler and supporting code to construct contexts for the component sub-models became redundant -- good. The approximate-repeats model was easily defined in terms of TimeSeriesS models, and further experimentation allowed it to be simplified by using time-series models of alignments.
Alignment Models, (OrBoth a b)
The data type [OrBoth a b] can be used to represent an alignment of two data series (sequences) [a] and [b]. Types a and b might or might not be the same depending on the application, for example it makes sense to align a sequence of DNA Codons, [(DNA,DNA,DNA)], with the AminoAcid sequence of a protein, [AminoAcid].
data OrBoth a b = JustL a | JustR b | Both a b
deriving (Eq, Ord, Read, Show)
modelOrBoth mO mA mB mAB =
let nlp (JustL a) = nlPr mO 0 + nlPr mA a
...
in MnlPr ... nlp ...
|
...ACG-... :: [DNA]
|
...A-AT... :: [DNA]
[... ||||
Both Ad Ad, ---.|||
JustL Cy, -----.||
Both Gu Ad, ---.|
JustR Ty, -----.
...] :: [OrBoth DNA DNA]
|
| 13 August 2004 |
(JustL and JustR are named after
Just, from the standard type
Forming a TimeSeries of (OrBoth a b)
A TimeSeries of (OrBoth a b) can be formed in many ways but
one natural way is from
a
tsmOrBoth combine tsmO tsmL tsmR = -- (was pairTSM)
let
c2m context = -- get predictions of the pieces
let
mO = context2model tsmO (orBothOs context) --of option
mA = context2model tsmL (orBothLs context) --of a
mB = context2model tsmR (orBothRs context) --of b, and
in modelOrBoth mO mA mB (combine mA mB) --glue them up
in TSM (msg1 tsmO + msg1 tsmL + msg1 tsmR) c2m
(\() -> "{tsmOrBoth " ++ show tsmO ++ "; "
++ show tsmL ++ "; " ++ show tsmR ++ "}" )
|
| mk2, 28/8/2004 |
(This required adding method
context2model ::
(tsm ds) ->
Finding a good [OrBoth a b]
Given a TimeSeries of (OrBoth a b) we can compare any
two alignments, i.e. two
The 2-D DPA
The 2-D
dynamic programming algorithm
(DPA) for finding the "cost" (or "score") of an optimal alignment of
two sequences, sa and sb,
under a variety of cost (score) measures, is well known and
some versions have even been programmed in
a lazy functional programming language[1].
In imperative languages it is usually described
in terms of a 2-D matrix, d[0..|sa|,0..|sb|],
where d[i,j] contains, possibly amongst other things,
the cost (score) of sa[0..i-1] and sb[0..j-1],
where sequence positions are numbered from zero.
The basic algorithm runs in
quadratic time provided that the calculation of
The 2-D DPA takes a time-series model
of
|
On Optimality
Note that in general taking a model of the population of sequences
into account can, and should, change
| model | alignment-1 | alignment-2 |
|---|---|---|
JustL JustR Both pr(0)=pr(1)=0.1, pr(2)=0.8; pr((x,x)|Both)=0.8, pr((x,y)|Both)=0.2, x<>y; pr(A)=pr(T)=0.4, pr(G)=pr(C)=0.1 |
AC-
|
-CA
|||
4.64---.||
3.97---.|
4.64---.
|
-AC
|
CA-
|||
6.64---.||
1.97---.|
6.64---. bits
|
These two alignments (others are possible) would have
equal costs or scores under many algorithms.
Here matching the rare Cs,
compared to matching the common As,
saves
Contexts
One way to recover an optimal alignment is for the DPA
to also store the best choice,
i.e. north-west, north or west, in d[i,j].
This chain (context) of options, starting from d[|sa|,|sb|] and
leading back to d[0,0],
gives an optimal alignment in reverse order.
For many natural time-series models, the incremental cost of
a single step, from the n.w., n. or w., depends on the context.
There are exponentially many paths (alignments) from
d[0,0] to d[i,j] so it is not feasible to
store information about all of them in d[i,j].
For an order-k Markov model
the incremental cost depends only on the previous k≥0 steps,
that is on the first k elements of the appropriate context;
anything beyond this horizon has no effect.
It is sufficient to store a best representative context in d[i,j]
for each such prefix.
There are upto 3k possible context-prefixes of
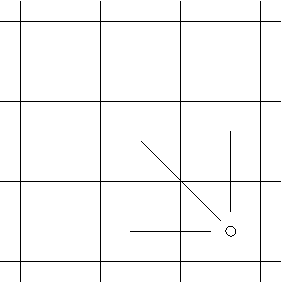
Shared length, k = 1, context prefixes,
appropriate for linear (affine) gap-costs.
There are upto three context-prefixes of length one, fewer at boundaries.
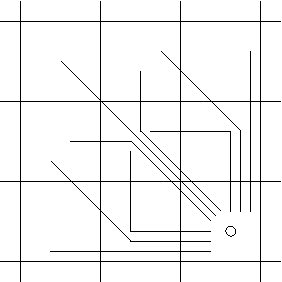
Shared length, k = 2, context prefixes.
There are upto nine context-prefixes of length two.
By storing only such representatives in d[i,j],
provided that the
Even for a time-series model with no bound on a "horizon", it may still be a good heuristic to store only such a collection of representative contexts for some k imposed by the programmer, the DPA then yielding good, but not necessarily optimal, alignments.
States
Some time-series models are based on
functions with state (and
it seems that the 2-D DPA can only achieve both
good efficiency and generality for such models).
Such a model does not look at the context
but rather at its current state and at the next data element.
Therefore a state must be stored with each representative context
(the context is still necessary to recover a final alignment).
The state could be recreated on demand by retracing an alignment,
class (TimeSeries tsm) => TimeSeriesS tsm where
step :: (tsm ds) -> ds -> (tsm ds) -- state trans'n
predict :: (tsm ds) -> ModelType ds
data TimeSeriesTypeS dataSpace =
forall state . TSMs MessageLength state
(state -> dataSpace -> state) -- trans'n
(state -> ModelType dataSpace) -- predict
(state -> String) -- show
tsmOrBoth combine tsmO tsmL tsmR = -- _, ops, a, b
let t (tsmO, tsmL, tsmR) (JustL a) =
((step tsmO 0), (step tsmL a), tsmR)
...
p (tsmO, tsmL, tsmR) =
let mA = predict tsmL
mB = predict tsmR
in modelOrBoth ... mA mB ...
in TSMs ... t p ...
|
| 14/10/2004 |
To use state-based time-series models
the DPA is required to store, for each "open" alternative
at the current position,
Approximate Repeats Models, 1 series
Some uncertainty remains about the best data-structure(s) for an approximate-repeats hypothesis; one redundant candidate is:
data ApproxRepeats a = Gen a | Jump Int | Rpt (OrBoth a a)
modelAppRpts mO mA mN mOB =
let nlp (Gen a) = nlPr mO 0 + nlPr mA a
nlp (Jump n) = nlPr mO 1 + nlPr mN n
nlp (Rpt ob) = nlPr mO 2 + nlPr mOB ob -- ob::OrBoth...
in MnlPr ... nlp ...
|
On Editing
The are various "models" of editing ([b]->[a]), e.g.
data Edit3 a = E3ins a | E3del | E3use a
-- NB x--(E3use y)-->y
data Edit4 a = E4ins a | E4del | E4chng a | E4copy
-- application determines if x--(E4chng x)-->x is legal
|
For no very strong reason,
[b] is the "source" and
[a] is the "target".
Edit3 or Edit4 can be used to give non-redundant representations of approximate-repeats.
There are some "cute" correspondences
([JustL|JustR|Both],[a],[b]) <--> [OrBoth a b] <--> ([b],[Edit3 a]) <--> ([b],[Edit4 a]) -- if applicable |
And there must be related correspondences on relevant statistical models.
Forming a TimeSeries of (ApproxRepeats a)
Given a suitable data structure,
the approximate-repeats time-series model follows a similar pattern
to the time-series model of
tsmApproxRepeats tsmO tsmA0 tsmO2 =
let
combine2 mA mB =
let cm = combine mA mB
p (a,b) = pr cm (a,b) / pr mB b -- NB b is given
in MPr ... p ...
t (n, tsmO, tsmA, tsmOB) (Gen a) = -- t, state trans'n
(n+1, step tsmO 0, step tsmA a, tsmOB)
t(n, tsmO, tsmA, _) (Jump _) =
(n, step tsmO 1, tsmA, tsmOrBoth combine2 tsmO2 tsmA tsmA0) --!
...
p (n, tsmO, tsmA, tsmOB) = -- state -> prediction
modelAppRpts (predict tsmO) -- "ops"
(predict tsmA) -- a
(uniform 0 (n-1)) -- say, Jumps
(predict tsmOB) -- OrBoth a a'
in TSMs ... (0, tsmO, tsmA0, tsmOrBoth combine2 tsmO2 tsmA0 tsmA0)
t p ...
|
| 14/10/, 24/10/2004 |
tsmO models the Gen|Jump|Rpt operations and
tsmO2 models the JustL|JustR|Both operations.
tsmA0 is the "base" model for elements of the series that are
output by Gen operations.
Note the use, twice, of tsmOrBoth...,
Classes
The class structure, from super to sub, could in principle get as complex as:
| class | instances | |
|---|---|---|
| super | TimeSeries predictors | TimeSeriesType |
| sub | TimeSeriesS step predict | TimeSeriesTypeS |
| sub2 | TimeSeries' context2model | TimeSeriesType' |
where TimeSeriesType' is ~ TimeSeriesType
augmented with an option to store a "state",
References
- [1] L. Allison,
Lazy Dynamic-Programming can be Eager.
Inf. Proc. Lett, 43(4), pp.207-212, Sept 1992.- [2] L. Allison, D. Powell & T. I. Dix, Compression and Approximate Matching.
Computer J., 42(1), pp.1-10, 1999.- [3] D. Powell, L. Allison & T. I. Dix, Modelling-Alignment for Non-Random Sequences.
17th Australian ComputerSoc. (ACS) Australian Joint Conf. on Artificial Intelligence (AI2004), Cairns Queensland, pp.203-214, Springer-Verlag,LNCS/LNAI vol.3339 ,6-10 Dec 2004 .- [4] L. Stern, L. Allison, R. L. Coppel & T. I. Dix, Discovering patterns in Plasmodium falciparum genomic DNA. Molecular and Biochemical Parasitology, 118(2), pp.175-186,
Dec 2001 (also see ,L. Allison ,T. Edgoose ,T. I. Dix , Compression of strings with approximate repeats. Intell. Sys. in Mol.Biol. '98 , pp.8-16,June 1998). - [2] L. Allison, D. Powell & T. I. Dix, Compression and Approximate Matching.
- Also see [more references].
|