Smoothed Particle Magnetohydrodynamics IV - Using the Vector Potential

Daniel J. Price

Accepted to MNRAS 14th Sep 2009 [ full text pdf (2.2Mb) ]

[ Paper I ][ Paper II ][ PhD Thesis ][ Paper III ][ Paper IV ]

Abstract

In this paper we investigate the use of the vector potential as a means of maintaining the divergence constraint in the numerical solution of the equations of Magnetohydrodynamics (MHD) using the Smoothed Particle Hydrodynamics (SPH) method. We derive a self-consistent formulation of the equations of motion using a variational principle that is constrained by the numerical formulation of both the induction equation and the curl operator used to obtain the magnetic field, which guarantees exact and simultaneous conservation of momentum, energy and entropy in the numerical scheme. This leads to a novel formulation of the MHD force term, unique to the vector potential, which differs from previous formulations. We also demonstrate how dissipative terms can be correctly formulated for the vector potential such that the contribution to the entropy is positive definite and the total energy is conserved.

On a standard suite of numerical tests in one, two and three dimensions we find firstly that the consistent formulation of the vector potential equations is unstable to the well-known SPH tensile instability, even more so than in the standard Smoothed Particle Magnetohydrodynamics (SPMHD) formulation where the magnetic field is evolved directly. Furthermore we find that, whilst a hybrid approach based on the vector potential evolution equation coupled with a standard force term gives good results for one and two dimensional problems (where dAz/dt = 0), such an approach suffers from numerical instability in three dimensions related to the unconstrained evolut ion of vector potential components. We conclude that use of the vector potential is not a viable approach for Smoothed Particle Magnetohydrodynamics.

Movies

[ click here to see all, click below for specific movies ]

	512x512 particle calculation of the Orszag-Tang Vortex problem in 2D using the hybrid vector potential approach. (31Mb Quicktime) This shows some of the advantages of the vector potential approach - in 2D very nice solutions can be obtained provided some simple corrections for numerical instabilities are implemented (see below). In 3D even this calculation has difficulties because the remaining two components of the vector potential (that are zero in 2D) grow exponentially with time. This is probably related to a requirement to enforce div A = 0 in 3D.
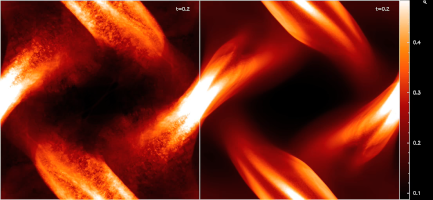
	Comparison of the energy conserving vector potential formulation (left) to a hybrid formulation using a standard SPMHD force (right) on the Orszag-Tang Vortex problem in 2D using 512x512 particles. (2.7Mb Quicktime) The energy conserving formulation is highly unstable to the SPH tensile instability -- yet remarkably conserves energy better than the movie on the right!
	Propagation of a non-linear circularly polarised Alfven wave in 2.5D, showing the particle distribution (left) and the x component of the magnetic field (right) (5.5Mb Quicktime) This shows the correct solution obtained when corrections for the SPH tensile instability are added. What happens in the absence of such corrections can be seen in the movie below.
	As above, but showing what happens if corrections for the tensile instability are not applied (6.7Mb Quicktime). The tensile instability manifests as a "clumping" of particles along the direction of the magnetic field lines. The physical reason for its occurrence in MHD is the presence of a component of magnetic force directed along the line of sight proportional to the divergence of the magnetic field (i.e., the presence of monopole terms in the numerical solution). These are fairly easily removed, as seen above, but results in slightly worse conservation of momentum (you judge which is better!).
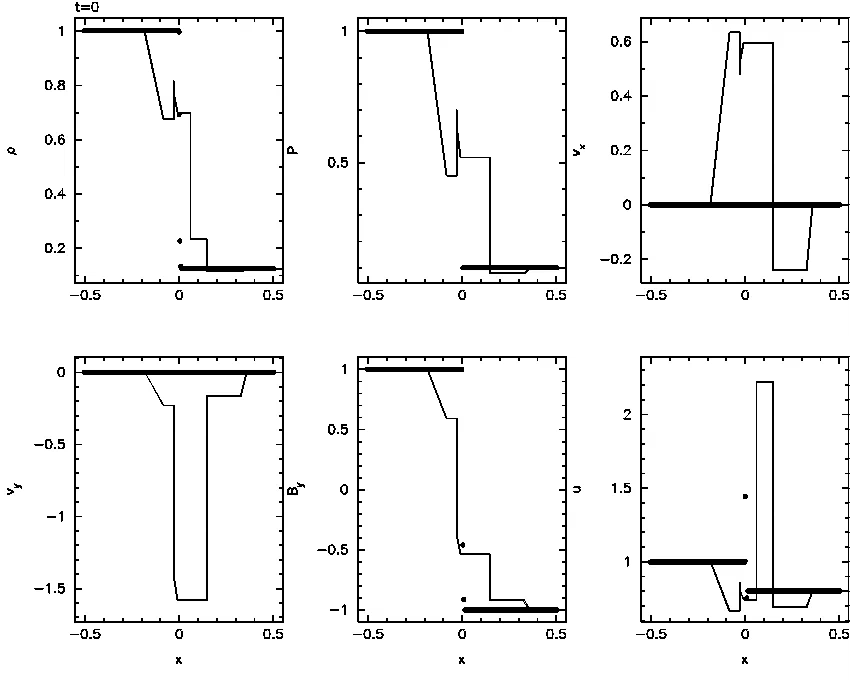
	The energy-conserving vector potential method on the Brio-Wu shock tube problem in 1.5D, with no corrections. (4.1Mb Quicktime) Also showing the truly disastrous consequences of the tensile instability if left unchecked. Yes it is this bad.