Example 1
| Example 1 |
Pupils might choose to test the distance of the bat tip past the crease line.
Using this starting point, the distance that the bat tip is past the crease-line is varied and the speed of the batsman is kept constant. The calculated times are compared with the time that the bail has been falling that pupils calculated in Lesson 2. A reasonable result is 0.165 s.
In this example the running speed is assumed to be 10 m/s and reasonable limits of between 0.1 m and 0.9 m are chosen for distance the bat tip is past the crease line. A spreadsheet can be used to calculate times for the bat tip to reach these various distances. A graph can be produced in Excel which shows that (at constant speed) the greater the assumed distance of the bat tip past the crease line, the longer it takes to go that distance.
Speed of batsman (m/s) | Distance past crease line (m) | Time (sec) |
|
|
10.00 | 0.10 | 0.010 |
| |
10.00 | 0.20 | 0.020 |
| |
10.00 | 0.30 | 0.030 |
| |
10.00 | 0.40 | 0.040 |
| |
10.00 | 0.50 | 0.050 |
| |
10.00 | 0.60 | 0.060 |
| |
10.00 | 0.70 | 0.070 |
| |
10.00 | 0.80 | 0.080 |
| |
10.00 | 0.90 | 0.090 |
|
The spreadsheet formulas are as follows:
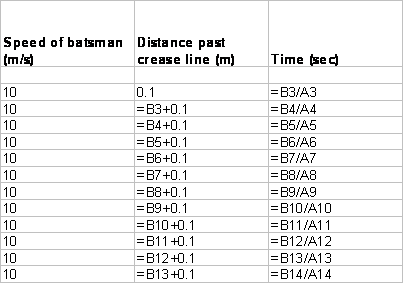
For THIS assumed speed of the batsman, the batsman is always OUT. This is because, in each case, the time that the bat tip has been past the crease line is less than the time the bail has been falling (0.165 s)
If you start with a different assumed speed, there may be results where the batsman is IN.
Speed of batsman (m/s) | Distance past crease line (m) | Time (sec) |
|
|
5.00 | 0.10 | 0.020 |
| |
5.00 | 0.20 | 0.040 |
| |
5.00 | 0.30 | 0.060 |
| |
5.00 | 0.40 | 0.080 |
| |
5.00 | 0.50 | 0.100 |
| |
5.00 | 0.60 | 0.120 |
| |
5.00 | 0.70 | 0.140 |
| |
5.00 | 0.80 | 0.160 |
| |
5.00 | 0.90 | 0.180 |
|
For THIS assumed speed of the batsman, the batsman is IN if the bat tip is assumed to be 0.90 m past the crease line. This is because the time that the bat tip has been past the crease line is equal to the time the bail has been falling (0.18 s).