Jump to main navigation

«
»

Workshop 4 - multiple and non-linear regression

22 May 2011

Basic statistics references

  • Logan (2010) - Chpt 9
  • Quinn & Keough (2002) - Chpt 6
Very basic overview of regression

Multiple Linear Regression

Paruelo & Lauenroth (1996) analyzed the geographic distribution and the effects of climate variables on the relative abundance of a number of plant functional types (PFT's) including shrubs, forbs, succulents (e.g. cacti), C3 grasses and C4 grasses. They used data from 73 sites across temperate central North America (see pareulo.syd) and calculated the relative abundance of C3 grasses at each site as a response variable

Download Paruelo data set

Format of paruelo.csv data file
C3LATLONGMAPJJAMAPDJFMAP
............

C3Relative abundance of C3 grasses at each site - response variable
LATLatitude in centesimal degrees - predictor variable
LONGLongitude in centesimal degrees - predictor variable
MAPMean annual precipitation (mm) - predictor variable
MATMean annual temperature (0C) - predictor variable
JJAMAPProportion of MAP that fell in June, July and August - predictor variable
DJFMAPProportion of MAP that fell in December, January and Febrary - predictor variable
Saltmarsh

Open
the paruelo data file. HINT.
Show code

> paruelo <- read.table("paruelo.csv", header = T, sep = ",", strip.white = T)

> head(paruelo)

    C3   LAT   LONG MAP  MAT JJAMAP DJFMAP
1 0.65 46.40 119.55 199 12.4   0.12   0.45
2 0.65 47.32 114.27 469  7.5   0.24   0.29
3 0.76 45.78 110.78 536  7.2   0.24   0.20
4 0.75 43.95 101.87 476  8.2   0.35   0.15
5 0.33 46.90 102.82 484  4.8   0.40   0.14
6 0.03 38.87  99.38 623 12.0   0.40   0.11

Q1-1. In the table below, list the assumptions of multiple linear regression along with how violations of each assumption are diagnosed and/or the risks of violations are minimized.
AssumptionDiagnostic/Risk Minimization
I.
II.
III.
IV.
V.


Q1-2. Construct a scatterplot matrix
to investigate these assumptions(HINT)
Show code

> library(car)

> scatterplotMatrix(~C3 + LAT + LONG + MAP + MAT + JJAMAP + DJFMAP,

> data = paruelo, diagonal = "boxplot")

> library(lattice)

> splom.lat <- splom(paruelo, type = c("p", "r"))

> print(splom.lat)

> library(ggplot2)

> splom.gg <- plotmatrix(paruelo) + geom_smooth(method = "lm")

> print(splom.gg)

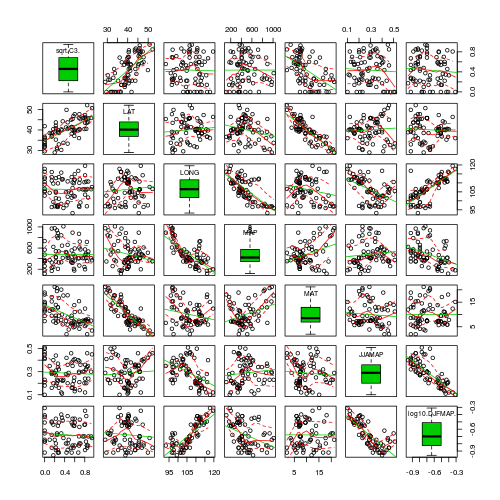
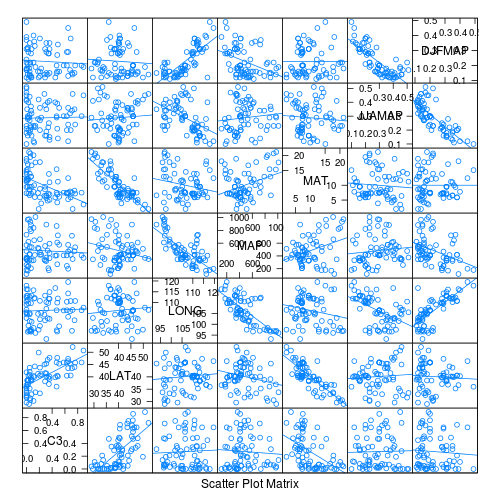
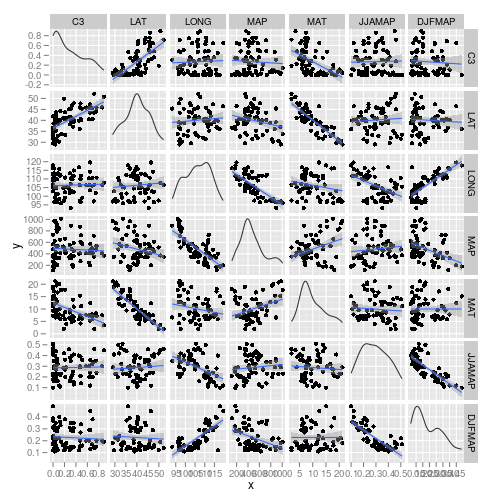
  1. Focussing on the assumptions of Normality, Homogeneity of Variance and Linearity, is there evidence of violations of these assumptions (y or n)?
  2. Try applying a temporary square root transformation (HINT). Does this improve some of these specific assumptions (y or n)?
    Show code

    > library(car)

    > scatterplotMatrix(~sqrt(C3) + LAT + LONG + MAP + MAT + JJAMAP +

    > log10(DJFMAP), data = paruelo, diagonal = "boxplot")

  3. Is there any evidence that the assumption of Collinearity is likely to be violated (y or n)?
  4. (Multi)collinearity
    occurs when one or more of the predictor variables are correlated to the other predictor variables, therefore this assumption can also be examined by calculating the pairwise correlation coefficients between all the predictor variables (HINT). Which predictor variables are highly correlated?
    Show code

    > cor(paruelo[, -1])

                   LAT        LONG        MAP          MAT      JJAMAP       DJFMAP
    LAT     1.00000000  0.09655281 -0.2465058 -0.838590413  0.07417497 -0.065124848
    LONG    0.09655281  1.00000000 -0.7336870 -0.213109100 -0.49155774  0.770743994
    MAP    -0.24650582 -0.73368703  1.0000000  0.355090766  0.11225905 -0.404512409
    MAT    -0.83859041 -0.21310910  0.3550908  1.000000000 -0.08077131  0.001478037
    JJAMAP  0.07417497 -0.49155774  0.1122590 -0.080771307  1.00000000 -0.791540381
    DJFMAP -0.06512485  0.77074399 -0.4045124  0.001478037 -0.79154038  1.000000000


Q1-3. Whilst the above diagnostics are useful at identifying potential (Multi)collinearity issues, they do not examine collinearity directly. (Multi)collinearity can more be diagnosed directly via tolerance and variance inflation factor (VIF) measures.

  1. Calculate the VIF values for each of the predictor variables (HINT).
  2. Calculate the tolerance values for each of the predictor variables (HINT).
    Show code

    > library(car)

    > vif(lm(sqrt(paruelo$C3) ~ LAT + LONG + MAP + MAT + JJAMAP + log10(DJFMAP),

    > data = paruelo))

              LAT          LONG           MAP           MAT        JJAMAP 
         3.560103      4.988318      2.794157      3.752353      3.194724 
    log10(DJFMAP) 
         5.467330 

    > library(car)

    > 1/vif(lm(sqrt(paruelo$C3) ~ LAT + LONG + MAP + MAT + JJAMAP +

    > log10(DJFMAP), data = paruelo))

              LAT          LONG           MAP           MAT        JJAMAP 
        0.2808908     0.2004684     0.3578897     0.2664995     0.3130161 
    log10(DJFMAP) 
        0.1829046 

    PredictorVIFTolerance
    LAT
    LONG
    MAP
    MAT
    JJAMAP
    log10(DJFMAP)
  3. Is there any evidence of (multi)collinearity, and if so, which variables are responsible for violations of this assumption?

We obviously cannot easily incorporate all 6 predictors into the one model, because of the collinearity problem. Paruelo and Lauenroth (1996) separated the predictors into two groups for their analyses. One group included LAT and LONG and the other included MAP, MAT, JJAMAP and DJFMAP. We will focus on the relationship between the square root relative abundance of C3 plants and latitude and longitude. This relationship will investigate the geographic pattern in abundance of C3 plants.



Q1-4. Just like Paruelo and Lauenroth (1996), we will fit the multiplicative model for LAT and LONG.
  1. Write out the full multiplicative model
  2. Check the assumptions of this linear model. In particular, check collinearity. HINT
    Show code

    > library(car)

    > scatterplotMatrix(~sqrt(C3) + LAT + LONG, data = paruelo, diagonal = "boxplot")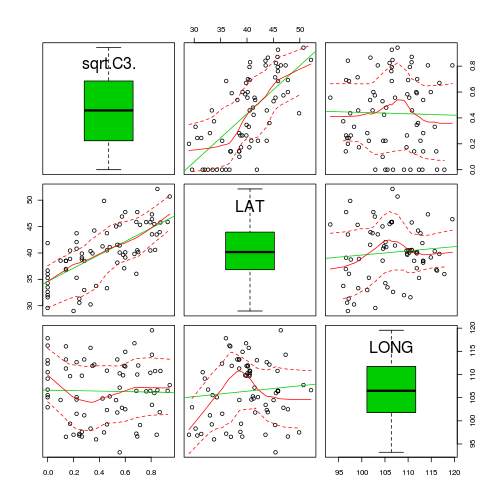

    > vif(lm(sqrt(C3) ~ LAT + LONG, data = paruelo))

        LAT    LONG 
    1.00941 1.00941 

  3. Obviously, this model will violate collinearity. It is highly likely that LAT and LONG will be related to the LAT:LONG interaction term. It turns out that if we center the variables, then the individual terms will no longer be correlated to the interaction. Center the LAT and LONG variables ( HINT) and (HINT)
    Show code

    > paruelo$cLAT <- scale(paruelo$LAT, scale = F)

    > paruelo$cLONG <- scale(paruelo$LONG, scale = F)



Q1-5. Fit a linear multiplicative model on the centered LAT and LONG ( HINT)
  1. Examine the diagnostic plots (HINT) specially the residual plot to confirm no further evidence of violations of the analysis assumptions
    Show code

    > paruelo.lm <- lm(sqrt(C3) ~ cLAT * cLONG, data = paruelo)

    > par(mfrow = c(2, 3), oma = c(0, 0, 2, 0))

    > plot(paruelo.lm, ask = F, which = 1:6)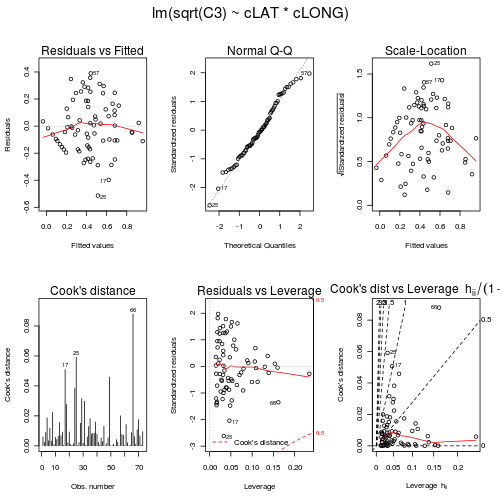

    > influence.measures(paruelo.lm)

    Influence measures of
     lm(formula = sqrt(C3) ~ cLAT * cLONG, data = paruelo) :
         dfb.1_  dfb.cLAT  dfb.cLON dfb.cLAT.    dffit cov.r   cook.d    hat inf
    1  -0.02402 -0.083059 -0.084079 -0.121467 -0.15232 1.379 5.88e-03 0.2347   *
    2  -0.02221 -0.064489 -0.040666 -0.073805 -0.09560 1.227 2.32e-03 0.1389   *
    3   0.08130  0.134833  0.066766  0.117108  0.18920 1.083 9.00e-03 0.0556    
    4   0.18842  0.102837 -0.149242 -0.074613  0.27640 0.957 1.87e-02 0.0317    
    5  -0.06669 -0.070090  0.046655  0.023640 -0.11683 1.091 3.45e-03 0.0448    
    6  -0.14663  0.020076  0.158421  0.006884 -0.21885 1.001 1.19e-02 0.0305    
    7  -0.06266  0.095315 -0.006186  0.047476 -0.11206 1.102 3.17e-03 0.0510    
    8  -0.14641  0.034868  0.221772 -0.071379 -0.30117 1.016 2.25e-02 0.0520    
    9  -0.03667  0.026450  0.024624 -0.005908 -0.05703 1.088 8.24e-04 0.0317    
    10 -0.14355 -0.014721  0.043712  0.016311 -0.15090 0.989 5.65e-03 0.0153    
    11 -0.06802 -0.077774  0.052091  0.030960 -0.12872 1.101 4.19e-03 0.0534    
    12 -0.09834  0.126501  0.005986  0.046997 -0.15816 1.064 6.29e-03 0.0388    
    13  0.11115 -0.093743 -0.111372  0.092157  0.24977 1.061 1.56e-02 0.0580    
    14  0.08474  0.046585 -0.103485 -0.077405  0.16432 1.104 6.81e-03 0.0622    
    15 -0.10466  0.005614  0.159085  0.003719 -0.19200 1.063 9.25e-03 0.0460    
    16  0.02997  0.006031 -0.022676 -0.007923  0.03832 1.082 3.72e-04 0.0234    
    17 -0.22231 -0.242042 -0.256005 -0.259471 -0.46135 0.867 5.07e-02 0.0464    
    18 -0.15718 -0.195191 -0.167613 -0.197664 -0.33555 0.980 2.77e-02 0.0483    
    19 -0.03827  0.067695  0.013203 -0.004632 -0.08826 1.133 1.97e-03 0.0703    
    20  0.14881  0.082543 -0.079749 -0.027279  0.19334 0.993 9.27e-03 0.0238    
    21  0.02694 -0.052154  0.013621 -0.042509  0.06315 1.184 1.01e-03 0.1064   *
    22  0.01333  0.036162  0.002225  0.019532  0.03980 1.165 4.02e-04 0.0911    
    23  0.03874 -0.041008 -0.026165  0.016163  0.07567 1.106 1.45e-03 0.0475    
    24  0.18953 -0.068780 -0.263543  0.120259  0.39649 0.949 3.83e-02 0.0522    
    25 -0.30655 -0.141051 -0.348442 -0.174237 -0.50904 0.721 5.92e-02 0.0333   *
    26 -0.01163  0.020739 -0.004288  0.014771 -0.02450 1.151 1.52e-04 0.0797    
    27 -0.06640 -0.035776  0.047618  0.021757 -0.09331 1.073 2.20e-03 0.0287    
    28  0.15820 -0.100195  0.156872 -0.087023  0.24687 1.004 1.51e-02 0.0371    
    29  0.23271 -0.199428  0.178733 -0.171942  0.36130 0.913 3.16e-02 0.0383    
    30 -0.05886 -0.051722  0.023280  0.001329 -0.08413 1.075 1.79e-03 0.0278    
    31  0.18206 -0.039000  0.294547 -0.009475  0.34876 0.977 2.98e-02 0.0503    
    32  0.04158  0.010092  0.004277  0.002215  0.04358 1.068 4.81e-04 0.0147    
    33 -0.11614  0.057069 -0.084317  0.045564 -0.15421 1.033 5.95e-03 0.0260    
    34  0.17140 -0.010972  0.149470  0.000787  0.22867 0.961 1.29e-02 0.0241    
    35  0.16157 -0.063790  0.207065 -0.047488  0.27074 0.999 1.81e-02 0.0405    
    36 -0.16599  0.051605  0.046986  0.028324 -0.17882 0.964 7.89e-03 0.0163    
    37 -0.09520  0.123426 -0.073860  0.112439 -0.18180 1.101 8.32e-03 0.0642    
    38 -0.12248  0.136168  0.016438  0.044325 -0.18258 1.034 8.33e-03 0.0325    
    39  0.21589  0.005332  0.135038  0.008527  0.25689 0.889 1.59e-02 0.0190    
    40 -0.15732 -0.003358 -0.079732 -0.002338 -0.17776 0.972 7.81e-03 0.0172    
    41 -0.08534  0.010451 -0.044041  0.007825 -0.09659 1.047 2.35e-03 0.0177    
    42 -0.03339  0.004442 -0.028421  0.002067 -0.04413 1.081 4.93e-04 0.0240    
    43  0.11153 -0.008546  0.093501 -0.001341  0.14632 1.030 5.36e-03 0.0234    
    44  0.06621  0.080305 -0.003529  0.027570  0.10631 1.074 2.85e-03 0.0321    
    45  0.14322  0.175378 -0.007707  0.060327  0.23128 0.999 1.33e-02 0.0324    
    46  0.00242  0.002970 -0.000135  0.001018  0.00392 1.096 3.89e-06 0.0325    
    47  0.04762  0.057578 -0.003518  0.018818  0.07632 1.084 1.47e-03 0.0321    
    48  0.09643  0.105320 -0.013197  0.027624  0.14620 1.048 5.37e-03 0.0294    
    49  0.21782  0.063120 -0.324557 -0.197238  0.43369 0.971 4.59e-02 0.0654    
    50 -0.00148  0.001425  0.002076 -0.003405 -0.00566 1.218 8.12e-06 0.1296   *
    51 -0.00449  0.005425  0.006061 -0.012462 -0.01985 1.262 1.00e-04 0.1598   *
    52  0.02355 -0.011871 -0.037630  0.035697  0.06961 1.160 1.23e-03 0.0885    
    53 -0.00616  0.005595  0.008294 -0.011850 -0.02099 1.190 1.12e-04 0.1093   *
    54  0.11316 -0.020147  0.059511 -0.015058  0.12914 1.024 4.18e-03 0.0181    
    55  0.08401 -0.006408  0.050234 -0.003848  0.09836 1.049 2.44e-03 0.0188    
    56  0.01263  0.000401  0.008831  0.000749  0.01556 1.081 6.14e-05 0.0203    
    57  0.23558  0.012600  0.162103  0.017720  0.28935 0.857 2.00e-02 0.0201    
    58  0.15162  0.005056  0.085545  0.005265  0.17570 0.979 7.64e-03 0.0181    
    59 -0.10917  0.059550 -0.109799  0.050149 -0.16684 1.050 6.98e-03 0.0349    
    60 -0.01928  0.010518 -0.019393  0.008857 -0.02947 1.097 2.20e-04 0.0349    
    61  0.07137 -0.085274 -0.078631  0.125075  0.23769 1.156 1.42e-02 0.1077    
    62 -0.05053  0.001789 -0.075856 -0.007046 -0.09174 1.096 2.13e-03 0.0434    
    63  0.00374  0.000609 -0.000752 -0.000272  0.00388 1.076 3.83e-06 0.0148    
    64 -0.03243 -0.005963  0.008964  0.002938 -0.03431 1.072 2.98e-04 0.0155    
    65 -0.17360 -0.059882  0.041757  0.006784 -0.19020 0.951 8.89e-03 0.0164    
    66 -0.21254 -0.161201  0.312816  0.383538 -0.59693 1.136 8.80e-02 0.1617    
    67  0.05944  0.032095 -0.092820 -0.099439  0.15603 1.217 6.16e-03 0.1367   *
    68 -0.03086  0.033212 -0.039691  0.034038 -0.06400 1.142 1.04e-03 0.0743    
    69 -0.08462  0.114424 -0.120547  0.127015 -0.20622 1.172 1.07e-02 0.1129    
    70 -0.12444  0.139820 -0.161230  0.144966 -0.26402 1.097 1.75e-02 0.0789    
    71 -0.09511  0.010274  0.128949 -0.001656 -0.16322 1.063 6.70e-03 0.0398    
    72  0.01563  0.003182 -0.030673 -0.027216  0.04310 1.251 4.71e-04 0.1534   *
    73 -0.06408 -0.180207  0.005698 -0.072658 -0.19407 1.154 9.51e-03 0.0995    

  2. All the diagnostics seem reasonable and present no indications that the model fitting and resulting hypothesis tests are likely to be unreliable. Complete the following table (HINT).
    Show code

    > summary(paruelo.lm)

    Call:
    lm(formula = sqrt(C3) ~ cLAT * cLONG, data = paruelo)
    Residuals:
         Min       1Q   Median       3Q      Max 
    -0.51312 -0.13427 -0.01134  0.14086  0.38940 
    Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
    (Intercept)  0.4282658  0.0234347  18.275  < 2e-16 ***
    cLAT         0.0436937  0.0048670   8.977 3.28e-13 ***
    cLONG       -0.0028773  0.0036842  -0.781   0.4375    
    cLAT:cLONG   0.0022824  0.0007471   3.055   0.0032 ** 
    ---
    Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
    Residual standard error: 0.1991 on 69 degrees of freedom
    Multiple R-squared: 0.5403, Adjusted R-squared: 0.5203 
    F-statistic: 27.03 on 3 and 69 DF,  p-value: 1.128e-11 

    CoefficientEstimatet-valueP-value
    Intercept
    cLAT
    cLONG
    cLAT:cLONG

Q1-6. Examine the partial regression plots of LAT and LONG (HINT).
Show code

> avPlots(paruelo.lm, ask = F, indentify.points = F)

> library(effects)

> plot(allEffects(paruelo.lm, default.levels = 5), ask = F)

> library(effects)

> plot(allEffects(lm(sqrt(C3) ~ cLONG * cLAT, data = paruelo),

> default.levels = 10), ask = F)

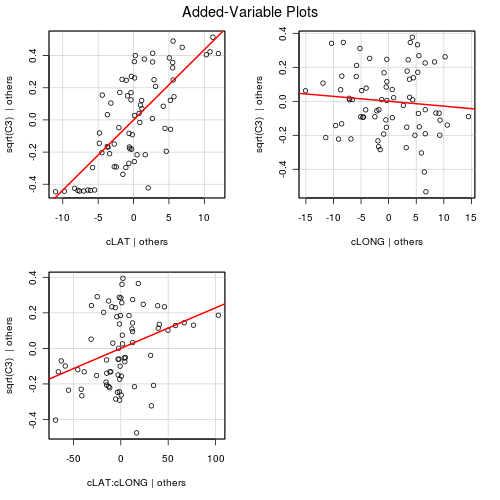
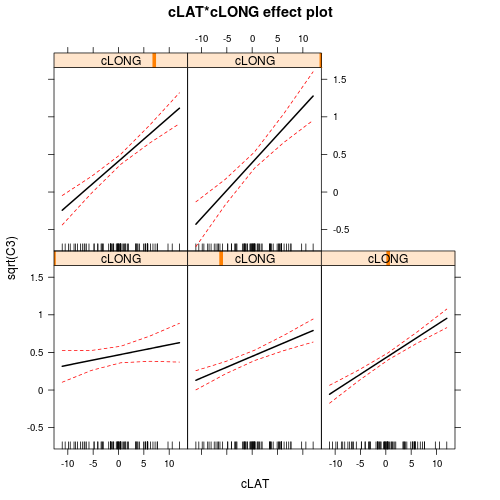
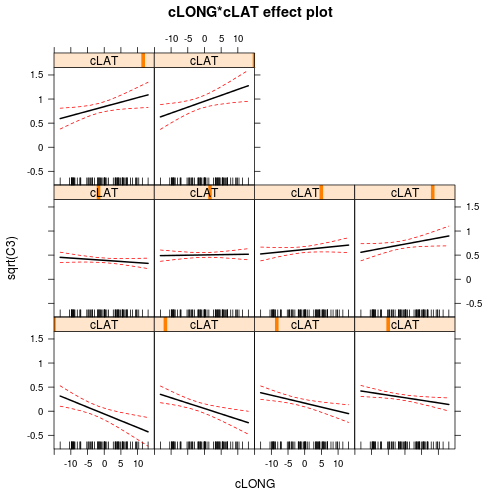
There is clearly an interaction between LAT and LONG. This indicates that the degree to which latitude effects the relative abundance of C3 plants depends on longitude and vice versa. The effects plots expressed for Latitude suggest that the relationship between relative C3 abundance and Latitude increases with increasing Longitude. The effects plots expressed for Longitude suggest that the relationship between relative C3 abundance and Longitude switch from negative at low Latitudes to positive at high Latitudes.

Q1-7. To investigate these patterns further, we will examine the simple effects of latitude at a specific range of longitudes. The levels of longitude that we will use are the mean longitude value as well as the mean plus or minus 1 SD and plus or minus 2 SD.
  1. Calculate the five levels of longitude on which the simple effects of latitude will be investigated. (HINT, HINT, etc).
    Show code

    > LongM2 <- mean(paruelo$cLONG) - 2 * sd(paruelo$cLONG)

    > LongM1 <- mean(paruelo$cLONG) - 1 * sd(paruelo$cLONG)

    > LongM <- mean(paruelo$cLONG)

    > LongP1 <- mean(paruelo$cLONG) + 1 * sd(paruelo$cLONG)

    > LongP2 <- mean(paruelo$cLONG) + 2 * sd(paruelo$cLONG)

  2. Investigate the simple effects of latitude on the relative abundance of C3 plants for each of these levels of longitude. (HINT), (HINT), etc).
    Show code

    > LatM2 <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG +

    > LongM2), data = paruelo))$coef["cLAT", ]

    > LatM1 <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG +

    > LongM1), data = paruelo))$coef["cLAT", ]

    > LatM <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG +

    > LongM), data = paruelo))$coef["cLAT", ]

    > LatP1 <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG +

    > LongP1), data = paruelo))$coef["cLAT", ]

    > LatP2 <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG +

    > LongP2), data = paruelo))$coef["cLAT", ]

    > rbind(`Lattitude at Long-2sd` = LatM2, `Lattitude at Long-1sd` = LatM1,

    > `Lattitude at mean Long` = LatM, `Lattitude at Long+1sd` = LatP1,

    > `Lattitude at Long+2sd` = LatP2)

                             Estimate  Std. Error  t value     Pr(>|t|)
    Lattitude at Long-2sd  0.07307061 0.012418103 5.884200 1.301574e-07
    Lattitude at Long-1sd  0.05838215 0.008113745 7.195463 5.877401e-10
    Lattitude at mean Long 0.04369369 0.004867032 8.977481 3.279384e-13
    Lattitude at Long+1sd  0.02900523 0.005270175 5.503657 5.926168e-07
    Lattitude at Long+2sd  0.01431678 0.008837028 1.620090 1.097748e-01


Multiple Linear Regression

Loyn (1987) modeled the abundance of forest birds with six predictor variables (patch area, distance to nearest patch, distance to nearest larger patch, grazing intensity, altitude and years since the patch had been isolated).

Download Loyn data set

Format of loyn.csv data file
ABUNDDISTLDISTAREAGRAZEALTYR.ISOL
..............

ABUNDAbundance of forest birds in patch- response variable
DISTDistance to nearest patch - predictor variable
LDISTDistance to nearest larger patch - predictor variable
AREASize of the patch - predictor variable
GRAZEGrazing intensity (1 to 5, representing light to heavy) - predictor variable
ALTAltitude - predictor variable
YR.ISOLNumber of years since the patch was isolated - predictor variable
Saltmarsh

Open the loyn data file. HINT.
Show code

> loyn <- read.table("loyn.csv", header = T, sep = ",", strip.white = T)

> head(loyn)

  ABUND AREA YR.ISOL DIST LDIST GRAZE ALT
1   5.3  0.1    1968   39    39     2 160
2   2.0  0.5    1920  234   234     5  60
3   1.5  0.5    1900  104   311     5 140
4  17.1  1.0    1966   66    66     3 160
5  13.8  1.0    1918  246   246     5 140
6  14.1  1.0    1965  234   285     3 130

Q2-1. In the table below, list the assumptions of multiple linear regression along with how violations of each assumption are diagnosed and/or the risks of violations are minimized.
AssumptionDiagnostic/Risk Minimization
I.
II.
III.
IV.
V.

Q2-2. Construct a scatterplot matrix
to investigate these assumptions(HINT)
Show code

> library(car)

> scatterplotMatrix(~ABUND + DIST + LDIST + AREA + GRAZE + ALT +

> YR.ISOL, data = loyn, diagonal = "boxplot")

> library(lattice)

> splom.lat <- splom(loyn, type = c("p", "r"))

> print(splom.lat)

%<>= %#via ggplot2 - warning these are slow! %library(ggplot2) %splom.gg <- plotmatrix(loyn)+geom_smooth(method="lm") %print(splom.gg) %@

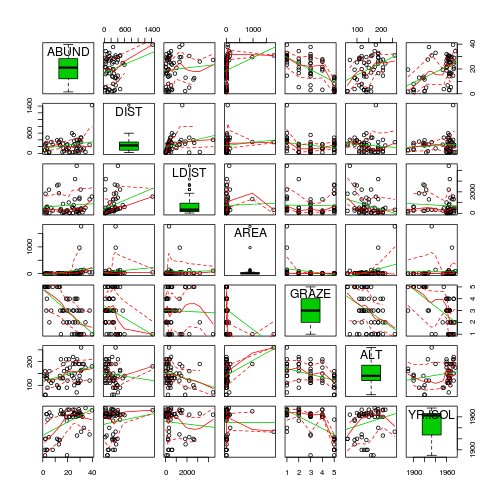
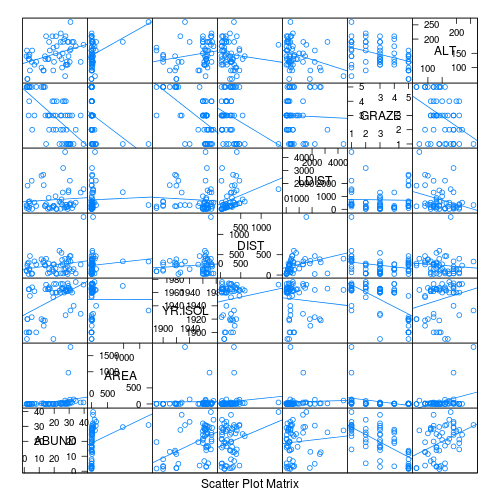
  1. Focussing on the assumptions of Normality, Homogeneity of Variance and Linearity, is there evidence of violations of these assumptions (y or n)?
  2. Try applying a temporary log10 transformation to the skewed variables(HINT).
    Show code

    > library(car)

    > scatterplotMatrix(~ABUND + log10(DIST) + log10(LDIST) + log10(AREA) +

    > GRAZE + ALT + YR.ISOL, data = loyn, diagonal = "boxplot")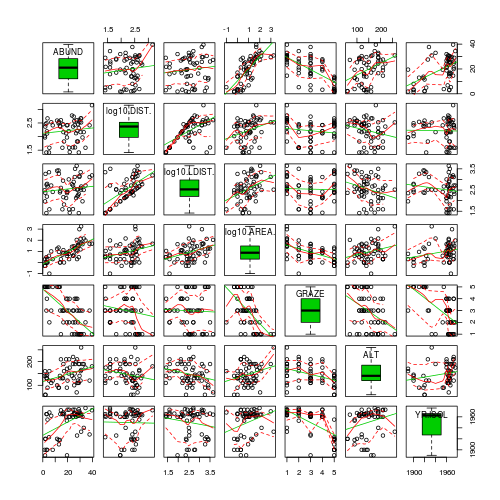

    Does this improve some of these specific assumptions (y or n)?
  3. Is there any evidence that the assumption of Collinearity is likely to be violated (y or n)?
    Show code

    > loyn.lm <- lm(ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) +

    > GRAZE + ALT + YR.ISOL, data = loyn)

    > vif(loyn.lm)

     log10(DIST) log10(LDIST)  log10(AREA)        GRAZE          ALT      YR.ISOL 
        1.654553     2.009749     1.911514     2.524814     1.467937     1.804769 

    > 1/vif(loyn.lm)

     log10(DIST) log10(LDIST)  log10(AREA)        GRAZE          ALT      YR.ISOL 
       0.6043930    0.4975746    0.5231454    0.3960688    0.6812282    0.5540876 


    PredictorVIFTolerance
    log10(DIST)
    log10(LDIST)
    log10(AREA)
    GRAZE
    ALT
    YR.ISOL
  4. Collinearity typically occurs when one or more of the predictor variables are correlated, therefore this assumption can also be examined by calculating the pairwise correlation coefficients between all the predictor variables (use transformed versions for those that required it) ( HINT).
    Show code

    > cor(loyn.lm$model[, 2:7])

                 log10(DIST) log10(LDIST) log10(AREA)       GRAZE        ALT
    log10(DIST)   1.00000000   0.60386637   0.3021666 -0.14263922 -0.2190070
    log10(LDIST)  0.60386637   1.00000000   0.3824795 -0.03399082 -0.2740438
    log10(AREA)   0.30216662   0.38247952   1.0000000 -0.55908864  0.2751428
    GRAZE        -0.14263922  -0.03399082  -0.5590886  1.00000000 -0.4071671
    ALT          -0.21900701  -0.27404380   0.2751428 -0.40716705  1.0000000
    YR.ISOL      -0.01957223  -0.16111611   0.2784145 -0.63556710  0.2327154
                     YR.ISOL
    log10(DIST)  -0.01957223
    log10(LDIST) -0.16111611
    log10(AREA)   0.27841452
    GRAZE        -0.63556710
    ALT           0.23271541
    YR.ISOL       1.00000000

    None of the predictor variables are overly correlated to any of the other predictor variables.

Since none of the predictor variables are highly correlated to one another, we can include all in the linear model fitting.

In this question, we are not so interested in hypothesis testing. That is, we are not trying to determine if there is a significant effect of one or more predictor variables on the abundance of forest birds. Rather, we wish to either (or both);

  • Construct a predictive model for relating habitat variables to forest bird abundances
  • Determine which are the most important (influential) predictor variables of forest bird abundances
As a result, a multiplicative model is unnecessary and overly complicated. For this purpose, an additive model (in which each of the predictors is included in the model without interaction terms) is appropriate.

Q2-3. Fit an additive linear model
relating ABUND to each of the predictor variables, but no interactions ( HINT)
Show code

> loyn.lm <- lm(ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) +

> GRAZE + ALT + YR.ISOL, data = loyn)


  1. Examine the diagnostic plots (HINT) specially the residual plot to confirm no further evidence of violations of the analysis assumptions
    Show code

    > par(mfrow = c(2, 3), oma = c(0, 0, 2, 0))

    > plot(loyn.lm, ask = F, which = 1:6)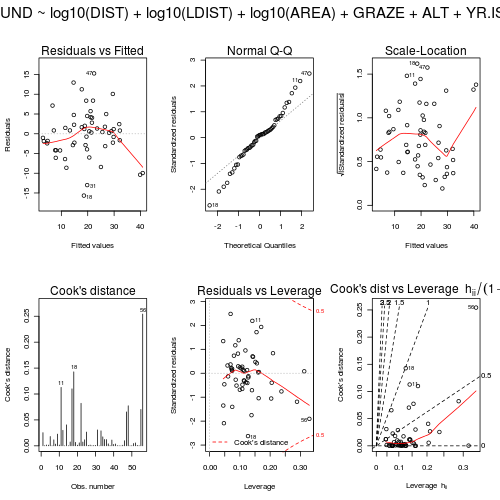

    > influence.measures(loyn.lm)

    Influence measures of
     lm(formula = ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) +      GRAZE + ALT + YR.ISOL, data = loyn) :
          dfb.1_ dfb.l10.D dfb.l10.L dfb.l10.A  dfb.GRAZ   dfb.ALT  dfb.YR.I
    1  -0.024547   0.08371 -0.022664  0.325348  0.219000 -0.005547  0.008468
    2  -0.017509  -0.01656  0.020997  0.012653  0.003658  0.037247  0.016013
    3  -0.058912   0.01045 -0.016321  0.048309  0.012241 -0.021952  0.060904
    4  -0.024649  -0.01083 -0.015504 -0.047360 -0.005965  0.010247  0.028327
    5   0.064514   0.17236 -0.075678 -0.091673  0.105181  0.101385 -0.078406
    6  -0.013955   0.01154  0.003907 -0.027075 -0.003667  0.000920  0.014184
    7   0.152729  -0.14223  0.018225  0.056318 -0.149535  0.022629 -0.148486
    8  -0.012535   0.00936 -0.059652  0.050580 -0.001515  0.058081  0.012466
    9   0.240434  -0.10307  0.040989  0.142365 -0.165009 -0.019501 -0.243854
    10 -0.049652  -0.03654 -0.001350  0.035981 -0.001217 -0.021708  0.054131
    11  0.326311  -0.29680  0.393485 -0.464543 -0.259851  0.555537 -0.347149
    12 -0.318813  -0.04143  0.184910 -0.047393  0.001434 -0.058520  0.324669
    13 -0.003880  -0.00858 -0.003634 -0.013295 -0.006816  0.013654  0.004853
    14  0.049590  -0.19049 -0.118128  0.391650  0.193189 -0.285935 -0.033841
    15  0.028372   0.01892 -0.019252  0.001533  0.002733 -0.003094 -0.029406
    16 -0.112157   0.03131 -0.058961  0.040297 -0.017552 -0.062221  0.119657
    17  0.089920  -0.36895 -0.418556  0.197950 -0.137942 -0.554335 -0.016929
    18  0.003210   0.44969  0.471153 -0.189555  0.055517  0.413749 -0.081604
    19 -0.014516  -0.05622 -0.077388  0.014877  0.026729  0.051520  0.021493
    20  0.031138   0.01561 -0.029390 -0.019603 -0.059824 -0.066354 -0.026445
    21 -0.074573   0.03497  0.084655 -0.115333  0.004721  0.153777  0.066229
    22  0.012462   0.62313 -0.547520  0.034210 -0.102778  0.004117 -0.020621
    23  0.007417   0.07767  0.112948 -0.066606  0.000558  0.110277 -0.024123
    24  0.057330   0.06179 -0.042947 -0.103211 -0.203842 -0.153868 -0.046055
    25  0.399742  -0.06158 -0.055316 -0.020120 -0.228704  0.012557 -0.400107
    26 -0.036316  -0.02478  0.062377 -0.032586  0.009891  0.023836  0.035302
    27  0.062196  -0.01369 -0.045659  0.029139 -0.023443 -0.004247 -0.061136
    28  0.022345  -0.01170  0.005156 -0.004665 -0.032184 -0.032509 -0.020565
    29 -0.048454   0.02411 -0.016234  0.017630  0.047216 -0.006470  0.048550
    30  0.020424   0.00550  0.013709  0.018552  0.021831 -0.019583 -0.022322
    31  0.181882  -0.18332  0.070644 -0.044548 -0.080909  0.204938 -0.188993
    32 -0.004554  -0.00646 -0.010581  0.012558  0.011367  0.000130  0.005339
    33 -0.192246   0.07100 -0.214312  0.246055  0.262466 -0.178104  0.205265
    34 -0.167748   0.08351 -0.072012  0.100394  0.263665  0.204739  0.156632
    35  0.056797  -0.06516  0.082675  0.005839  0.006404 -0.128022 -0.056773
    36 -0.136228  -0.06411  0.004602  0.101551  0.082178 -0.132967  0.148678
    37  0.004153  -0.01116 -0.045478 -0.053435 -0.081659  0.014926  0.001372
    38 -0.010846  -0.04066  0.048479 -0.013496 -0.004557  0.016275  0.010883
    39 -0.222802   0.01356  0.109160  0.039879  0.210745  0.089951  0.214317
    40 -0.005977   0.01113 -0.036499 -0.056239 -0.058831  0.032006  0.008643
    41 -0.031032  -0.08019  0.031978  0.020113  0.089394  0.033669  0.030566
    42 -0.029798   0.03356 -0.007763  0.018255  0.027276 -0.002476  0.028465
    43  0.001060  -0.00833  0.008234 -0.000729  0.011017 -0.007667 -0.001249
    44  0.004393  -0.00930  0.000714  0.002619 -0.009448 -0.010691 -0.003254
    45  0.011664   0.03240 -0.064340  0.046954 -0.013554 -0.053380 -0.008156
    46 -0.044055   0.00853 -0.126785  0.175238  0.125507  0.057840  0.045178
    47  0.348086  -0.09628  0.068676  0.328440 -0.113019 -0.256880 -0.347655
    48 -0.139098   0.50451  0.055716 -0.138456 -0.085820  0.270712  0.103904
    49  0.000830   0.00124  0.009247 -0.002171 -0.015170 -0.005737 -0.000635
    50  0.010389   0.02638 -0.015605  0.006676 -0.022689 -0.000897 -0.010726
    51 -0.048345  -0.13467  0.071349  0.066280  0.022910  0.002208  0.053729
    52 -0.019314   0.04851 -0.061717 -0.025118  0.088505  0.129007  0.012520
    53 -0.000455  -0.00517 -0.030151 -0.009949  0.025032 -0.004643  0.001860
    54  0.032378  -0.00621 -0.010783  0.019668 -0.025119 -0.000179 -0.031927
    55  0.072633  -0.00990 -0.045849 -0.458184 -0.072288 -0.111714 -0.060767
    56 -0.524582  -0.31857  0.429361 -0.754208  0.024705 -0.528460  0.569683
         dffit cov.r   cook.d    hat inf
    1  -0.4206 1.395 2.55e-02 0.2374    
    2  -0.0657 1.319 6.29e-04 0.1279    
    3  -0.1103 1.288 1.77e-03 0.1150    
    4   0.0998 1.217 1.45e-03 0.0690    
    5   0.3575 1.036 1.81e-02 0.0849    
    6   0.0385 1.243 2.16e-04 0.0734    
    7  -0.2837 1.250 1.16e-02 0.1399    
    8  -0.1520 1.289 3.36e-03 0.1247    
    9  -0.4029 0.937 2.27e-02 0.0748    
    10 -0.1064 1.286 1.65e-03 0.1132    
    11  0.9263 0.653 1.13e-01 0.1413    
    12 -0.4586 1.179 3.00e-02 0.1620    
    13  0.0364 1.302 1.93e-04 0.1142    
    14 -0.5334 1.236 4.06e-02 0.2036    
    15  0.0490 1.295 3.50e-04 0.1105    
    16 -0.2278 1.199 7.50e-03 0.0998    
    17  0.9038 0.798 1.10e-01 0.1704    
    18 -1.0674 0.459 1.43e-01 0.1268   *
    19  0.2163 1.162 6.75e-03 0.0804    
    20  0.0950 1.281 1.31e-03 0.1078    
    21  0.1998 1.318 5.80e-03 0.1513    
    22 -0.7615 1.323 8.21e-02 0.2888    
    23 -0.2259 1.218 7.38e-03 0.1079    
    24  0.2864 1.253 1.18e-02 0.1419    
    25  0.4310 1.320 2.67e-02 0.2095    
    26  0.0810 1.209 9.54e-04 0.0591    
    27 -0.1034 1.178 1.55e-03 0.0487    
    28 -0.0462 1.322 3.11e-04 0.1281    
    29  0.0678 1.284 6.70e-04 0.1053    
    30  0.0809 1.272 9.54e-04 0.0998    
    31 -0.4816 0.632 3.08e-02 0.0472    
    32  0.0235 1.380 8.04e-05 0.1630    
    33  0.4545 0.968 2.89e-02 0.0962    
    34  0.3493 1.149 1.75e-02 0.1183    
    35 -0.2959 0.929 1.23e-02 0.0452    
    36  0.2943 0.930 1.22e-02 0.0449    
    37 -0.1651 1.254 3.96e-03 0.1085    
    38  0.0559 1.679 4.56e-04 0.3127   *
    39  0.2799 1.260 1.13e-02 0.1435    
    40 -0.1378 1.287 2.76e-03 0.1204    
    41 -0.1590 1.221 3.67e-03 0.0888    
    42  0.0597 1.236 5.19e-04 0.0714    
    43 -0.0327 1.228 1.56e-04 0.0611    
    44  0.0161 1.376 3.79e-05 0.1604    
    45  0.0934 1.260 1.27e-03 0.0943    
    46  0.2630 1.157 9.95e-03 0.0936    
    47  0.7168 0.485 6.55e-02 0.0693   *
    48  0.7515 0.885 7.74e-02 0.1550    
    49  0.0297 1.246 1.28e-04 0.0746    
    50  0.0536 1.242 4.18e-04 0.0744    
    51  0.1778 1.335 4.60e-03 0.1561    
    52 -0.1989 1.421 5.75e-03 0.2052    
    53 -0.0817 1.251 9.72e-04 0.0862    
    54  0.0506 1.315 3.73e-04 0.1240    
    55 -0.7173 0.853 7.03e-02 0.1384    
    56 -1.3723 1.007 2.54e-01 0.3297   *

  2. On initial examination of the fitted model summary, which of the predictor variables might you consider important? (this can initially be determined by exploring which of the effects are significant?)
    Show code

    > summary(loyn.lm)

    Call:
    lm(formula = ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) + 
        GRAZE + ALT + YR.ISOL, data = loyn)
    Residuals:
         Min       1Q   Median       3Q      Max 
    -15.6506  -2.9390   0.5289   2.5353  15.2842 
    Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
    (Intercept)  -125.69725   91.69228  -1.371   0.1767    
    log10(DIST)    -0.90696    2.67572  -0.339   0.7361    
    log10(LDIST)   -0.64842    2.12270  -0.305   0.7613    
    log10(AREA)     7.47023    1.46489   5.099 5.49e-06 ***
    GRAZE          -1.66774    0.92993  -1.793   0.0791 .  
    ALT             0.01951    0.02396   0.814   0.4195    
    YR.ISOL         0.07387    0.04520   1.634   0.1086    
    ---
    Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
    Residual standard error: 6.384 on 49 degrees of freedom
    Multiple R-squared: 0.6849, Adjusted R-squared: 0.6464 
    F-statistic: 17.75 on 6 and 49 DF,  p-value: 8.443e-11 


    CoefficientEstimatet-valueP-value
    Intercept
    log10(DIST)
    log10(LDIST)
    log10(AREA)
    GRAZE
    ALT
    YR.ISOL

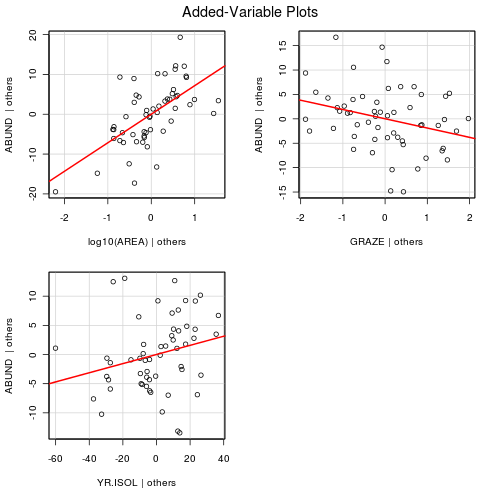
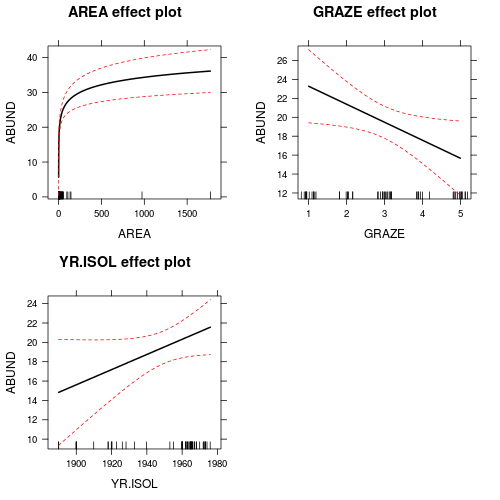
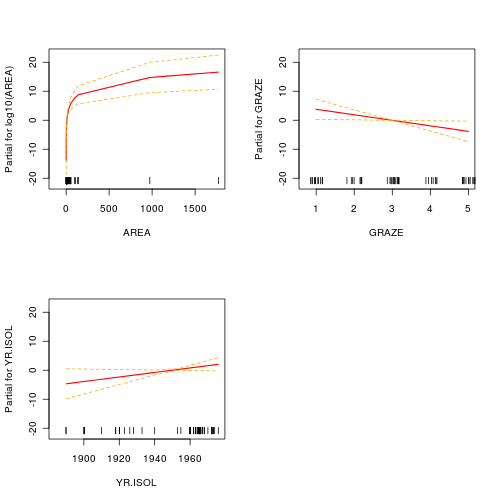
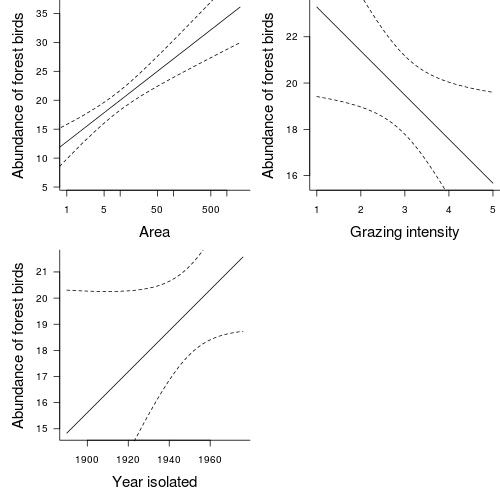
Clearly, not all of the predictor variables have significant partial effects on the abundance of forest birds. In developing a predictive model for relating forest bird abundances to a range of habitat characteristics, not all of the measured variables are useful. Likewise, the measured variables are not likely to be equally influential in determining the abundance of forest birds.

Q2-4. We would now like to be able to find the 'best' regression model.
Calculate the adjusted r2 (HINT), generic AIC (HINT) and generic BIC (HINT) for the full regression containing all six predictor variables.
Show code

> summary(loyn.lm)$adj.r.squared

[1] 0.6463567

> AIC(loyn.lm)

[1] 375.0638

> AIC(loyn.lm, k = log(nrow(loyn)))

[1] 391.2666


ModelAdj. r2AICBIC
Full

Q2-5. Compare all possible models and select the 'best' (most parsimonious) model
based on AIC and investigate the importance of each of the predictor variables using model averaging (HINT).
Show code

> library(MuMIn)

> model.avg(get.models(dredge(loyn.lm, rank = "AIC"), subset = delta <=

> 100))

Call:  model.avg(object = get.models(dredge(loyn.lm, rank = "AIC"), 
    subset = delta <= 100))
Component models: 
‘2+3+6’       ‘1+2+3+6’     ‘2+3+5+6’     ‘2+3+4+6’     
‘2+3’         ‘2+3+5’       ‘1+3+6’       ‘1+2+3’       
‘2+3+4’       ‘1+2+3+4+6’   ‘1+2+3+5+6’   ‘2+3+4+5+6’   
‘3+6’         ‘1+2+3+5’     ‘2+3+4+5’     ‘1+2+3+4’     
‘1+3+5+6’     ‘3+5+6’       ‘1+3+4+6’     ‘1+2+3+4+5+6’ 
‘3+4+6’       ‘1+2+3+4+5’   ‘1+3+4+5+6’   ‘3+4+5+6’     
‘1+3’         ‘1+3+5’       ‘3+5’         ‘1+3+4’       
‘1+3+4+5’     ‘3+4+5’       ‘3’           ‘3+4’         
‘2’           ‘1+2+5+6’     ‘1+2+5’       ‘1+2’         
‘2+5’         ‘2+6’         ‘1+2+6’       ‘2+5+6’       
‘2+4’         ‘1+2+4’       ‘1+2+4+5+6’   ‘1+2+4+5’     
‘1+2+4+6’     ‘2+4+5’       ‘2+4+6’       ‘2+4+5+6’     
‘1+5+6’       ‘1+4+5+6’     ‘1+4+6’       ‘1+6’         
‘5+6’         ‘6’           ‘4+6’         ‘4+5+6’       
‘1+5’         ‘1+4’         ‘1+4+5’       ‘1’           
‘null’        ‘4’           ‘5’           ‘4+5’        
Coefficients: 
          ALT         GRAZE   (Intercept)   log10(AREA)   log10(DIST) 
   0.01067846   -1.73394090 -102.20213305    7.54506989   -0.51843439 
 log10(LDIST)       YR.ISOL 
  -0.52644064    0.06194771 

  1. The model that you would consider to be the most parsimonious would be the model containing which terms?
  2. Use the model averaging to estimate the regression coefficients for each term.
    Predictor:EstimateSELower 95% CIUpper 95% CI
    log10 patch distance
    log10 large patch distance
    log10 fragment area
    Grazing intensity
    Altitude
    Years of isolation
    Intercept
Q2-6. Write out the full predictive model relating the abundance of forest birds to habitat characteristics based on:
  • the model averaging
  • refitting the most parsimonious model
    Show code

    > loyn.lm1 <- lm(ABUND ~ log10(AREA) + GRAZE + YR.ISOL, data = loyn)

    > summary(loyn.lm1)

    Call:
    lm(formula = ABUND ~ log10(AREA) + GRAZE + YR.ISOL, data = loyn)
    Residuals:
         Min       1Q   Median       3Q      Max 
    -14.5159  -3.8136   0.2027   3.1271  14.5542 
    Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
    (Intercept) -134.26065   86.39085  -1.554   0.1262    
    log10(AREA)    7.16617    1.27260   5.631 7.32e-07 ***
    GRAZE         -1.90216    0.87447  -2.175   0.0342 *  
    YR.ISOL        0.07835    0.04340   1.805   0.0768 .  
    ---
    Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
    Residual standard error: 6.311 on 52 degrees of freedom
    Multiple R-squared: 0.6732, Adjusted R-squared: 0.6544 
    F-statistic: 35.71 on 3 and 52 DF,  p-value: 1.135e-12 

Q2-7. Examine the partial effects plots.
Show code

> library(car)

> avPlots(loyn.lm1, ask = F)

> library(effects)

> plot(allEffects(loyn.lm1, default.levels = 1000), ask = F)

> par(mfrow = c(2, 2))

> termplot(loyn.lm1, se = T, rug = T, ask = F)

> library(effects)

> loyn.effects <- allEffects(loyn.lm1, default.levels = 1000)

> opar <- par(mfrow = c(2, 2))

> par(mar = c(5, 5, 0, 0))

> eff <- loyn.effects$"log10(AREA)"

> with(eff, plot(fit[, 1] ~ x[, 1], log = "x", xlim = c(1, 2000),

> type = "l", ann = F, axes = F))

> with(eff, points(upper[, 1] ~ x[, 1], type = "l", lty = 2))

> with(eff, points(lower[, 1] ~ x[, 1], type = "l", lty = 2))

> axis(1)

> mtext("Area", 1, line = 3, cex = 1.25)

> axis(2, las = 1)

> mtext("Abundance of forest birds", 2, line = 3, cex = 1.25)

> box(bty = "l")

> eff <- loyn.effects$GRAZE

> par(mar = c(5, 5, 0, 0))

> with(eff, plot(fit[, 1] ~ x[, 1], type = "l", ann = F, axes = F))

> with(eff, points(upper[, 1] ~ x[, 1], type = "l", lty = 2))

> with(eff, points(lower[, 1] ~ x[, 1], type = "l", lty = 2))

> axis(1)

> mtext("Grazing intensity", 1, line = 3, cex = 1.25)

> axis(2, las = 1)

> mtext("Abundance of forest birds", 2, line = 3, cex = 1.25)

> box(bty = "l")

> eff <- loyn.effects$YR.ISOL

> par(mar = c(5, 5, 0, 0))

> with(eff, plot(fit[, 1] ~ x[, 1], type = "l", ann = F, axes = F))

> with(eff, points(upper[, 1] ~ x[, 1], type = "l", lty = 2))

> with(eff, points(lower[, 1] ~ x[, 1], type = "l", lty = 2))

> axis(1)

> mtext("Year isolated", 1, line = 3, cex = 1.25)

> axis(2, las = 1)

> mtext("Abundance of forest birds", 2, line = 3, cex = 1.25)

> box(bty = "l")

> par(opar)

Polynomial regression

Rademaker and Cerqueira (2006), compiled data from the literature on the reproductive traits of opossoms (Didelphis) so as to investigate latitudinal trends in reproductive output. In particular, they were interested in whether there were any patterns in mean litter size across a longitudinal gradient from 44oN to 34oS. Analyses of data compiled from second hand sources are called metaanalyses and are very usefull at revealing overal trends across a range of studies.

Download Rademaker data set

Format of rademaker.csv data files
SPECIESLATITUDEL/YMAOPMLSREFERENCE
D.v.44216.88.4Tyndale-Biscoe and Mackenzie (1976)
D.v.411.514.19.4Hossler et al. (1994)
D.v.41.5??8.6Reynolds (1952)
D.v.412189Wiseman and Hendrickson (1950)
D.v.40215.87.9Sanderson (1961)
..................

SPECIESDidelphid species (D.al.=Didelphis albiventris, D.au.=Didelphis aurita, D.m.=Didelphis marsupialis, D.v.=Didelphis virginiana - Descriptor variable
LATITUDELattitude (degees) of study site - Predictor variable
L/YMean number of litter per year - Response variable
MAOPMean annual offspring production - Response variable
MLSMean litter size - Response variable
REFERENCEOriginal source of data
opossum

Open the rademaker data file.
Show code

> rademaker <- read.table("rademaker.csv", header = T, sep = ",",

> strip.white = T)

> head(rademaker)

  SPECIES LATITUDE L.Y MAOP MLS         DB                           REFERENCE
1    D.v.     44.0 2.0 16.8 8.4 M-Feb-Sept Tyndale-Biscoe and Mackenzie (1976)
2    D.v.     41.0 1.5 14.1 9.4 E-Mar-Sept               Hossler et al. (1994)
3    D.v.     41.5  NA   NA 8.6                                Reynolds (1952)
4    D.v.     41.0 2.0 18.0 9.0 M-Feb-Sept      Wiseman and Hendrickson (1950)
5    D.v.     40.0 2.0 15.8 7.9 M-Feb-Sept                    Sanderson (1961)
6    D.v.     39.0 2.0 17.8 8.9 E-Feb-Sept                     Reynolds (1945)

The main variables of interest in this data set are MLS (mean litter size) and LATITUDE. The other variables were included so as to enable you to see how meta data might be collected and collated from a number of other sources.

The relationship between two continuous variables can be analyzed by simple linear regression. Before performing the analysis we need to check the assumptions. To evaluate the assumptions of linearity, normality and homogeneity of variance, construct a scatterplot
of MLS against LATITUDE including a lowess smoother and boxplots on the axes. (HINT)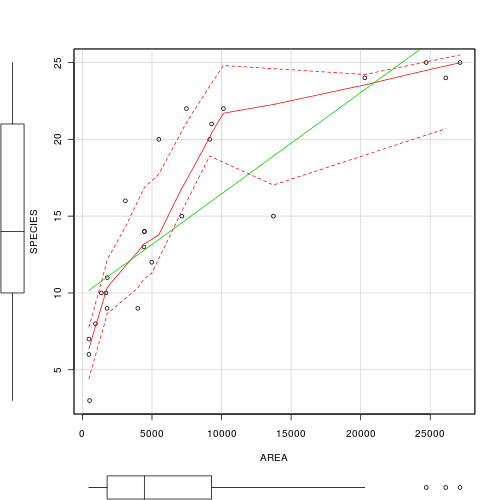
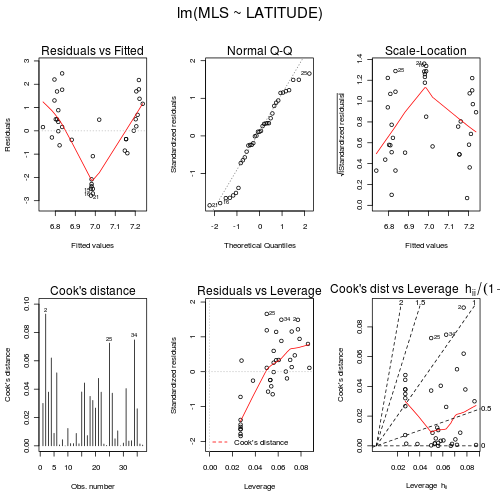
Show code

> library(car)

> scatterplot(MLS ~ LATITUDE, data = rademaker)

Q3-1. Is there any evidence that any of the regular assumptions of simple linear regression are likely to be violated?

To get an appreciation of what a residual plot would look like when there is some evidence that the linearity assumption has been violated, perform the simple linear regression (by fitting a linear model)
purely for the purpose of examining the regression diagnostics
(particularly the residual plot)
Show code

> rademaker.lm <- lm(MLS ~ LATITUDE, data = rademaker)

> par(mfrow = c(2, 3), oma = c(0, 0, 2, 0))

> plot(rademaker.lm, ask = F, which = 1:6)

> influence.measures(rademaker.lm)

Influence measures of
 lm(formula = MLS ~ LATITUDE, data = rademaker) :
      dfb.1_  dfb.LATI    dffit cov.r   cook.d    hat inf
1   0.094628  0.201743  0.24356 1.118 3.00e-02 0.0861    
2   0.185879  0.354286  0.43929 1.007 9.30e-02 0.0773    
3   0.114708  0.222842  0.27499 1.093 3.79e-02 0.0787    
4   0.150114  0.286119  0.35477 1.053 6.20e-02 0.0773    
5   0.057329  0.105129  0.13168 1.131 8.87e-03 0.0745    
6   0.144545  0.254834  0.32264 1.057 5.15e-02 0.0719    
7   0.016273  0.028690  0.03632 1.141 6.79e-04 0.0719    
8   0.041857  0.072336  0.09210 1.133 4.35e-03 0.0705    
9   0.000616  0.001001  0.00130 1.135 8.68e-07 0.0667    
10 -0.085085 -0.111051 -0.15544 1.095 1.23e-02 0.0552    
11 -0.031444 -0.039138 -0.05583 1.116 1.60e-03 0.0531    
12 -0.031444 -0.039138 -0.05583 1.116 1.60e-03 0.0531    
13 -0.076087 -0.090187 -0.13132 1.096 8.79e-03 0.0512    
14  0.049708  0.009612  0.05345 1.084 1.47e-03 0.0279    
15 -0.278150  0.002187 -0.28314 0.925 3.80e-02 0.0270    
16 -0.302666  0.002380 -0.30809 0.899 4.44e-02 0.0270    
17 -0.117656  0.000925 -0.11977 1.057 7.27e-03 0.0270    
18 -0.267330  0.012377 -0.27036 0.939 3.49e-02 0.0271    
19 -0.255295  0.011820 -0.25819 0.951 3.21e-02 0.0271    
20 -0.231553  0.010721 -0.23418 0.973 2.67e-02 0.0271    
21 -0.317516  0.020735 -0.32026 0.887 4.76e-02 0.0271    
22 -0.280153  0.018295 -0.28257 0.927 3.79e-02 0.0271    
23 -0.046707  0.026910 -0.05012 1.097 1.29e-03 0.0380    
24  0.021524 -0.017109  0.02524 1.115 3.28e-04 0.0500    
25  0.333540 -0.265117  0.39106 0.947 7.25e-02 0.0500    
26  0.234031 -0.186021  0.27439 1.027 3.72e-02 0.0500    
27 -0.082266  0.069901 -0.09893 1.109 5.01e-03 0.0540    
28  0.118457 -0.103838  0.14428 1.100 1.06e-02 0.0561    
29 -0.002004  0.001757 -0.00244 1.123 3.07e-06 0.0561    
30  0.051315 -0.044982  0.06250 1.118 2.01e-03 0.0561    
31  0.231543 -0.209119  0.28565 1.043 4.04e-02 0.0582    
32  0.066101 -0.059700  0.08155 1.118 3.41e-03 0.0582    
33  0.067544 -0.062775  0.08440 1.121 3.65e-03 0.0605    
34  0.311295 -0.297381  0.39396 0.991 7.48e-02 0.0628    
35  0.180242 -0.172186  0.22811 1.081 2.62e-02 0.0628    
36 -0.039381  0.039625 -0.05112 1.134 1.34e-03 0.0677    
37  0.023962 -0.028153  0.03388 1.160 5.91e-04 0.0873    

Q3-2. How would you describe the residual plot?

For this sort of trend that is clearly non-linear (yet the boxplots suggest normal data), transformations are of no use. Therefore, rather than attempt to model the data on a simple linear relationship (straight line), it is better to attempt to model the data on a curvilinear linear relationship (curved line). Note it is important to make the distinction between line (relationship) linearity and model linearity

Q3-3. If the assumptions are otherwise met, perform the second order polynomial regression analysis ( fit the quadratic polynomial model
), examine the output, and use the information to construct the regression equation relating the number of mean litter size to latitude:
Show code

> rademaker.lm <- lm(MLS ~ LATITUDE + I(LATITUDE^2), data = rademaker)

> rademaker.lm

Call:
lm(formula = MLS ~ LATITUDE + I(LATITUDE^2), data = rademaker)
Coefficients:
  (Intercept)       LATITUDE  I(LATITUDE^2)  
     5.391575      -0.029758       0.002448  

DV=intercept+slope1xIV2+slope2xIV
Mean litter size   =     +     x   latitude2   +     x   latitude

Q3-4. In polynomial regression, there are two hypotheses of interest. Firstly, as there are two slopes, we are now interested in whether the individual slopes are equal to one another and to zero
(that is, does the overall model explain our data better than just a horizontal line (no trend). Secondly, we are interested in whether the second order polynomial model fits the data any better than a simple first order (straight-line) model
. Test these null hypotheses.
Show code

> summary(rademaker.lm)

Call:
lm(formula = MLS ~ LATITUDE + I(LATITUDE^2), data = rademaker)
Residuals:
    Min      1Q  Median      3Q     Max 
-2.3335 -0.6117 -0.1748  0.4688  2.4592 
Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)    5.391574   0.290622  18.552  < 2e-16 ***
LATITUDE      -0.029758   0.008385  -3.549  0.00115 ** 
I(LATITUDE^2)  0.002448   0.000368   6.653 1.24e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Residual standard error: 1.019 on 34 degrees of freedom
Multiple R-squared: 0.5711, Adjusted R-squared: 0.5459 
F-statistic: 22.64 on 2 and 34 DF,  p-value: 5.624e-07 

> rademaker.lm1 <- lm(MLS ~ LATITUDE, data = rademaker)

> anova(rademaker.lm, rademaker.lm1)

Analysis of Variance Table
Model 1: MLS ~ LATITUDE
Model 2: MLS ~ LATITUDE + I(LATITUDE^2)
  Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
1     35 81.311                                  
2     34 35.322  1    45.989 44.267 1.237e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 


  1. The slopes significantly different from one another and to 0 (F = , df = ,, P = )
  2. The second order polynomial regression model fit the data significantly better than a first order (straight line) regression model (F = , FONT face=Courier>df = ,, P = )

Q3-5. What are your conclusions (statistical and biological)?

Q3-6. Such an outcome might also be accompanied by a scatterpoint that illustrates the relationship between the mean litter size and latitude. Construct a scatterplot without a smoother or marginal boxplots (HINT). Include a quadratic (second order) trendline on this graph (HINT).
Show code

> opar <- par(mfrow = c(2, 2))

> opar1 <- par(mar = c(5, 5, 0, 0))

> plot(MLS ~ LATITUDE, data = rademaker, ann = F, axes = F, type = "n")

> points(MLS ~ LATITUDE, data = rademaker, col = "grey", pch = 16)

> xs <- with(rademaker, seq(min(LATITUDE), max(LATITUDE), l = 1000))

> ys <- predict(rademaker.lm, data.frame(LATITUDE = xs), interval = "confidence")

> points(ys[, "fit"] ~ xs, col = "black", type = "l")

> points(ys[, "lwr"] ~ xs, col = "black", type = "l", lty = 2)

> points(ys[, "upr"] ~ xs, col = "black", type = "l", lty = 2)

> axis(1)

> mtext("Lattitude", 1, line = 3, cex = 1.2)

> axis(2, las = 1)

> mtext(expression(paste("Mean litter size (", phantom() %+-% 95,

> "% CI)")), 2, line = 3, cex = 1.2)

> box(bty = "l")

> par(opar1)

> opar1 <- par(mar = c(5, 5, 0, 0))

> plot(MLS ~ LATITUDE, data = rademaker, ann = F, axes = F, type = "n")

> points(MLS ~ LATITUDE, data = rademaker, col = "grey", pch = 16)

> xs <- with(rademaker, seq(min(LATITUDE), max(LATITUDE), l = 1000))

> ys <- predict(rademaker.lm, data.frame(LATITUDE = xs), interval = "prediction")

> points(ys[, "fit"] ~ xs, col = "black", type = "l")

> points(ys[, "lwr"] ~ xs, col = "black", type = "l", lty = 2)

> points(ys[, "upr"] ~ xs, col = "black", type = "l", lty = 2)

> axis(1)

> mtext("Lattitude", 1, line = 3, cex = 1.2)

> axis(2, las = 1)

> mtext(expression(paste("Mean litter size (", phantom() %+-% 95,

> "% PI)")), 2, line = 3, cex = 1.2)

> box(bty = "l")

> par(opar1)

> opar1 <- par(mar = c(5, 5, 0, 0))

> plot(MLS ~ LATITUDE, data = rademaker, ann = F, axes = F, type = "n")

> points(MLS ~ LATITUDE, data = rademaker, col = "grey", pch = 16)

> xs <- with(rademaker, seq(min(LATITUDE), max(LATITUDE), l = 1000))

> ys <- predict(rademaker.lm, data.frame(LATITUDE = xs), se.fit = T)

> points(ys$fit ~ xs, col = "black", type = "l")

> points(ys$fit - ys$se.fit ~ xs, col = "black", type = "l", lty = 2)

> points(ys$fit + ys$se.fit ~ xs, col = "black", type = "l", lty = 2)

> axis(1)

> mtext("Lattitude", 1, line = 3, cex = 1.2)

> axis(2, las = 1)

> mtext(expression(paste("Mean litter size (", phantom() %+-% 1,

> "SE)")), 2, line = 3, cex = 1.2)

> box(bty = "l")

> par(opar1)

> opar1 <- par(mar = c(5, 5, 0, 0))

> plot(MLS ~ LATITUDE, data = rademaker, ann = F, axes = F, type = "n")

> points(MLS ~ LATITUDE, data = rademaker, col = "grey", pch = 16)

> xs <- with(rademaker, seq(min(LATITUDE), max(LATITUDE), l = 1000))

> ys <- predict(rademaker.lm, data.frame(LATITUDE = xs), se.fit = T)

> points(ys$fit ~ xs, col = "black", type = "l")

> points(ys$fit - 2 * ys$se.fit ~ xs, col = "black", type = "l",

> lty = 2)

> points(ys$fit + 2 * ys$se.fit ~ xs, col = "black", type = "l",

> lty = 2)

> axis(1)

> mtext("Lattitude", 1, line = 3, cex = 1.2)

> axis(2, las = 1)

> mtext(expression(paste("Mean litter size (", phantom() %+-% 2,

> "SE)")), 2, line = 3, cex = 1.2)

> box(bty = "l")

> par(opar1)

> par(opar)


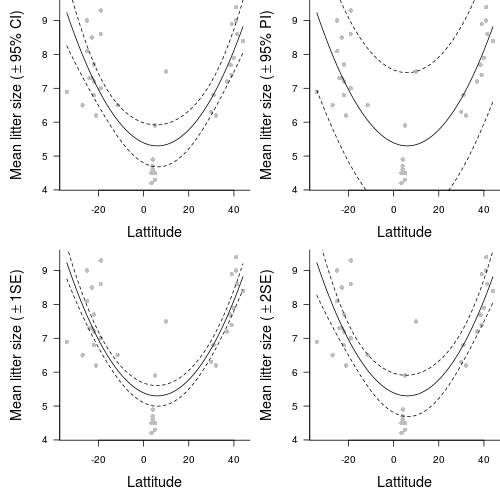
Nonlinear Regression

Peake and Quinn (1993) investigated the relationship between the size of mussel clumps (m2) and the number of other invertebrate species supported.

Download Peake data set

Format of peake.csv data file
AREASPECIESINDIV
516.0318
469.06760
462.25657
.........

AREAArea of the mussel clump (m2)- predictor variable
SPECIESNumber of other invertebrate species found in the mussel clumps - response variable
INDIVNumber of other invertebrate individuals found in the mussel clumps - ignore this response variable
Mussels

Open the peake data file. HINT.
Show code

> peake <- read.table("peake.csv", header = T, sep = ",", strip.white = T)

> head(peake)

     AREA SPECIES INDIV
1  516.00       3    18
2  469.06       7    60
3  462.25       6    57
4  938.60       8   100
5 1357.15      10    48
6 1773.66       9   118

Q4-1. For this question we will focus on an examination of the relationship between the number of species occupying a mussel clump and the size of the mussel clump. Construct a scatterplot
to investigate the assumptions of simple linear regression(HINT)
Show code

> library(car)

> scatterplot(SPECIES ~ AREA, data = peake)



  1. Focussing on the assumptions of Normality, Homogeneity of Variance and Linearity, is there evidence of violations of these assumptions (y or n)?


Q4-2. Although we could try a logarithmic transformation of the AREA variable, species/area curves are known to be non-linear. We might expect that small clumps would only support a small number of species. However, as area increases, there should be a dramatic increase in the number of species supported. Finally, further increases in area should see the number of species approach an asymptote. Species-area data are often modeled with non-linear functions:
  1. Try fitting a second order polynomial trendline
    through these data. E.g. Species = α*Area + β*Area2 + c (note that this is just an extension of y=mx+c)
    Show code

    > peake.lm <- lm(SPECIES ~ AREA + I(AREA^2), data = peake)

  2. Try fitting a power trendline
    through these data. E.g. Species = α(Area)β where the number of Species is proportional to the Area to the power of some coefficient (β).
    Show code

    > peake.nls <- nls(SPECIES ~ alpha * AREA^beta, data = peake, start = list(alpha = 0.1,

    > beta = 1))

  3. Try fitting an asymptotic exponential relationship through these data. E.g. Species = α-βeγArea.
    Show code

    > peake.nls1 <- nls(SPECIES ~ SSasymp(AREA, a, b, c), data = peake)



Q4-3. Compare the fit (via AIC, MSresidual and ANOVA) of each of the alternatives (also include the regular linear regression model).
Show code

> peake.lmLin <- lm(SPECIES ~ AREA, data = peake)

> AIC(peake.lmLin)

[1] 141.0756

> deviance(peake.lmLin)/df.residual(peake.lmLin)

[1] 14.13324

> AIC(peake.lm)

[1] 129.5497

> deviance(peake.lm)/df.residual(peake.lm)

[1] 8.601553

> anova(peake.lmLin, peake.lm)

Analysis of Variance Table
Model 1: SPECIES ~ AREA
Model 2: SPECIES ~ AREA + I(AREA^2)
  Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
1     23 325.06                                  
2     22 189.23  1    135.83 15.791 0.0006429 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

> AIC(peake.nls)

[1] 125.1312

> deviance(peake.nls)/df.residual(peake.nls)

[1] 7.468933

> AIC(peake.nls1)

[1] 125.7644

> deviance(peake.nls1)/df.residual(peake.nls1)

[1] 7.393005

> anova(peake.nls, peake.nls1)

Analysis of Variance Table
Model 1: SPECIES ~ alpha * AREA^beta
Model 2: SPECIES ~ SSasymp(AREA, a, b, c)
  Res.Df Res.Sum Sq Df Sum Sq F value Pr(>F)
1     23     171.78                         
2     22     162.65  1 9.1394  1.2362 0.2782

ModelAICMSresidP-value
Species = β*Area + c Compare linear and polynomial
in the box below
Species = α*Area + β*Area2 + c
Species = α(Area)β Compare power and asymptotic exponential
in the box below
Species = α-βeγArea

Selecting the most appropriate model to relate the number of species to mussel clump area now becomes a combination of both inferential signals and theoretical biology/ecology. Our knowledge of biology tells us that it is nonsense to suggest that continual mussel clump size increases will result in further linear increases in the number of species encountered. Whilst it is possible that species numbers could reach an maximum at an optimum clump area, the polynomial fit (whilst empirically better than a linear fit - lower AIC and MSresid), is only marginally more suitable. The power and asymptotic exponential models both fit the data substantially (significantly?? - some argue that AIC values 2 units lower are significantly lower) better than either of the linear models. The two non-linear models were not found to differ significantly from one another (in terms of ANOVA or AIC), yet arguably the exponential model that indicates the species numbers rise faster before eventually plateauing off might be considered a more realistic model.

Q4-4. Create a plot of species number against mussel clump area. Actually, this might be a good point to plot each of the competing models on separate sub-figures. Hence we will go through the process of building up the four sub-figures in a grid in the one larger figure.
  1. Start by setting up some whole figure (graphics device) parameters. In particular, indicate that the overall figure is going to comprise 2 rows and 2 columns.
    Show code

    > opar <- par(mfrow = c(2, 2))

  2. Setup the margins (5 units on the bottom and left and 0 units on the top and right) and dimensions of the blank plotting space. Also add the raw observations as solid grey dots
    Show code

    > opar1 <- par(mar = c(5, 5, 0, 0))

    > plot(SPECIES ~ AREA, data = peake, ann = F, axes = F, type = "n")

    > points(SPECIES ~ AREA, data = peake, col = "grey", pch = 16)

  3. Use the predict function to generate predicted (fitted) values and 95% confidence intervals for 1000 new AREA values between the minimum and maximum original AREA range. Plot the trend and confidence intervals in solid and dotted lines respectively.
    Show code

    > xs <- with(peake, seq(min(AREA), max(AREA), l = 1000))

    > ys <- predict(peake.lmLin, data.frame(AREA = xs), interval = "confidence")

    > points(ys[, "fit"] ~ xs, col = "black", type = "l")

    > points(ys[, "lwr"] ~ xs, col = "black", type = "l", lty = 2)

    > points(ys[, "upr"] ~ xs, col = "black", type = "l", lty = 2)

  4. Add axes, axes titles and a "L" shape axes box to the plot to complete the first sub-figure
    Show code

    > axis(1, cex.axis = 0.75)

    > mtext(expression(paste("Clump area", (dm^2))), 1, line = 3, cex = 1.2)

    > axis(2, las = 1, cex.axis = 0.75)

    > mtext(expression(paste("Number of species (", phantom() %+-%

    > 95, "%CI)")), 2, line = 3, cex = 1.2)

    > box(bty = "l")

    > par(opar1)

  5. Complete the second sub-figure (polynomial trend) in much the same manner as the first (linear trend)
    Show code

    > opar1 <- par(mar = c(5, 5, 0, 0))

    > plot(SPECIES ~ AREA, data = peake, ann = F, axes = F, type = "n")

    > points(SPECIES ~ AREA, data = peake, col = "grey", pch = 16)

    > xs <- with(peake, seq(min(AREA), max(AREA), l = 1000))

    > ys <- predict(peake.lm, data.frame(AREA = xs), interval = "confidence")

    > points(ys[, "fit"] ~ xs, col = "black", type = "l")

    > points(ys[, "lwr"] ~ xs, col = "black", type = "l", lty = 2)

    > points(ys[, "upr"] ~ xs, col = "black", type = "l", lty = 2)

    > axis(1, cex.axis = 0.75)

    > mtext(expression(paste("Clump area", (dm^2))), 1, line = 3, cex = 1.2)

    > axis(2, las = 1, cex.axis = 0.75)

    > mtext(expression(paste("Number of species (", phantom() %+-%

    > 95, "%CI)")), 2, line = 3, cex = 1.2)

    > box(bty = "l")

    > par(opar1)

  6. Start the third (power) model similarly
    Show code

    > opar1 <- par(mar = c(5, 5, 0, 0))

    > plot(SPECIES ~ AREA, data = peake, ann = F, axes = F, type = "n")

    > points(SPECIES ~ AREA, data = peake, col = "grey", pch = 16)

  7. Estimating confidence intervals is a little more complex for non-linear least squares models as the predict() function does not yet support calculating standard errors or intervals. Nevertheless, we can do this manually (go R you good thing!).
    1. Firstly we need to refit the non-linear power model incorporating a function that will be used to specify gradient calculations. This will be necessary to form the basis of SE calculations. So the gradient needs to be specified using the deriv3() function.
    2. Secondly, we then refit the power model using this new gradient function
    Show code

    > grad <- deriv3(~alpha * AREA^beta, c("alpha", "beta"), function(alpha,

    > beta, AREA) NULL)

    > peake.nls <- nls(SPECIES ~ grad(alpha, beta, AREA), data = peake,

    > start = list(alpha = 0.1, beta = 1))

  8. The predicted values of the trend as well as standard errors can then be calculated and used to plot approximate 95% confidence intervals. One standard error is equivalent to approximately 68% confidence intervals. The conversion between standard error and 95% confidence interval follows the formula 95%CI=1.96xSE. Actually, 1.96 (or 2) is an approximation from large (>30) sample sizes. A more exact solution can be obtained by multiplying the SE by pt(0.975,df) where df is the degrees of freedom.
    Show code

    > ys <- predict(peake.nls, data.frame(AREA = xs))

    > se.fit <- sqrt(apply(attr(predict(peake.nls1, list(AREA = xs)),

    > "gradient"), 1, function(x) sum(vcov(peake.nls1) * outer(x,

    > x))))

    > points(ys ~ xs, col = "black", type = "l")

    > points(ys + 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

    > points(ys - 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

  9. Finish sub-figure 3 similar to the other two
    Show code

    > points(ys + 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

    > points(ys - 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

    > axis(1, cex.axis = 0.75)

    > mtext(expression(paste("Clump area", (dm^2))), 1, line = 3, cex = 1.2)

    > axis(2, las = 1, cex.axis = 0.75)

    > mtext(expression(paste("Number of species", (phantom() %+-% 2 ~

    > SE), )), 2, line = 3, cex = 1.2)

    > box(bty = "l")

    > par(opar1)

  10. Sub-figure four (asymptotic exponential) is similar to the power model except that as it already incorporates a gradient function (SSasymp()), this step is not required.
    Show code

    > opar1 <- par(mar = c(5, 5, 0, 0))

    > plot(SPECIES ~ AREA, data = peake, ann = F, axes = F, type = "n")

    > points(SPECIES ~ AREA, data = peake, col = "grey", pch = 16)

    > xs <- with(peake, seq(min(AREA), max(AREA), l = 1000))

    > ys <- predict(peake.nls1, data.frame(AREA = xs))

    > se.fit <- sqrt(apply(attr(ys, "gradient"), 1, function(x) sum(vcov(peake.nls1) *

    > outer(x, x))))

    > points(ys ~ xs, col = "black", type = "l")

    > points(ys + 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

    > points(ys - 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

    > axis(1, cex.axis = 0.75)

    > mtext(expression(paste("Clump area", (dm^2))), 1, line = 3, cex = 1.2)

    > axis(2, las = 1, cex.axis = 0.75)

    > mtext(expression(paste("Number of species", (phantom() %+-% 2 ~

    > SE), )), 2, line = 3, cex = 1.2)

    > box(bty = "l")

    > par(opar1)

  11. Finally, finalize the figure by restoring the plotting (graphics device) parameters
    Show code

    > par(opar)

To see the entire figure generating code, and the figure itself...
Show code

> opar <- par(mfrow = c(2, 2))

> opar1 <- par(mar = c(5, 5, 0, 0))

> plot(SPECIES ~ AREA, data = peake, ann = F, axes = F, type = "n")

> points(SPECIES ~ AREA, data = peake, col = "grey", pch = 16)

> xs <- with(peake, seq(min(AREA), max(AREA), l = 1000))

> ys <- predict(peake.lmLin, data.frame(AREA = xs), interval = "confidence")

> points(ys[, "fit"] ~ xs, col = "black", type = "l")

> points(ys[, "lwr"] ~ xs, col = "black", type = "l", lty = 2)

> points(ys[, "upr"] ~ xs, col = "black", type = "l", lty = 2)

> axis(1, cex.axis = 0.75)

> mtext(expression(paste("Clump area", (dm^2))), 1, line = 3, cex = 1.2)

> axis(2, las = 1, cex.axis = 0.75)

> mtext(expression(paste("Number of species (", phantom() %+-%

> 95, "%CI)")), 2, line = 3, cex = 1.2)

> box(bty = "l")

> par(opar1)

> opar1 <- par(mar = c(5, 5, 0, 0))

> plot(SPECIES ~ AREA, data = peake, ann = F, axes = F, type = "n")

> points(SPECIES ~ AREA, data = peake, col = "grey", pch = 16)

> xs <- with(peake, seq(min(AREA), max(AREA), l = 1000))

> ys <- predict(peake.lm, data.frame(AREA = xs), interval = "confidence")

> points(ys[, "fit"] ~ xs, col = "black", type = "l")

> points(ys[, "lwr"] ~ xs, col = "black", type = "l", lty = 2)

> points(ys[, "upr"] ~ xs, col = "black", type = "l", lty = 2)

> axis(1, cex.axis = 0.75)

> mtext(expression(paste("Clump area", (dm^2))), 1, line = 3, cex = 1.2)

> axis(2, las = 1, cex.axis = 0.75)

> mtext(expression(paste("Number of species (", phantom() %+-%

> 95, "%CI)")), 2, line = 3, cex = 1.2)

> box(bty = "l")

> par(opar1)

> opar1 <- par(mar = c(5, 5, 0, 0))

> plot(SPECIES ~ AREA, data = peake, ann = F, axes = F, type = "n")

> points(SPECIES ~ AREA, data = peake, col = "grey", pch = 16)

> xs <- with(peake, seq(min(AREA), max(AREA), l = 1000))

> grad <- deriv3(~alpha * AREA^beta, c("alpha", "beta"), function(alpha,

> beta, AREA) NULL)

> peake.nls <- nls(SPECIES ~ grad(alpha, beta, AREA), data = peake,

> start = list(alpha = 0.1, beta = 1))

> ys <- predict(peake.nls, data.frame(AREA = xs))

> se.fit <- sqrt(apply(attr(predict(peake.nls1, list(AREA = xs)),

> "gradient"), 1, function(x) sum(vcov(peake.nls1) * outer(x,

> x))))

> points(ys ~ xs, col = "black", type = "l")

> points(ys + 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

> points(ys - 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

> axis(1, cex.axis = 0.75)

> mtext(expression(paste("Clump area", (dm^2))), 1, line = 3, cex = 1.2)

> axis(2, las = 1, cex.axis = 0.75)

> mtext(expression(paste("Number of species", (phantom() %+-% 2 ~

> SE), )), 2, line = 3, cex = 1.2)

> box(bty = "l")

> par(opar1)

> opar1 <- par(mar = c(5, 5, 0, 0))

> plot(SPECIES ~ AREA, data = peake, ann = F, axes = F, type = "n")

> points(SPECIES ~ AREA, data = peake, col = "grey", pch = 16)

> xs <- with(peake, seq(min(AREA), max(AREA), l = 1000))

> ys <- predict(peake.nls1, data.frame(AREA = xs))

> se.fit <- sqrt(apply(attr(ys, "gradient"), 1, function(x) sum(vcov(peake.nls1) *

> outer(x, x))))

> points(ys ~ xs, col = "black", type = "l")

> points(ys + 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

> points(ys - 2 * se.fit ~ xs, col = "black", type = "l", lty = 2)

> axis(1, cex.axis = 0.75)

> mtext(expression(paste("Clump area", (dm^2))), 1, line = 3, cex = 1.2)

> axis(2, las = 1, cex.axis = 0.75)

> mtext(expression(paste("Number of species", (phantom() %+-% 2 ~

> SE), )), 2, line = 3, cex = 1.2)

> box(bty = "l")

> par(opar1)

> par(opar)



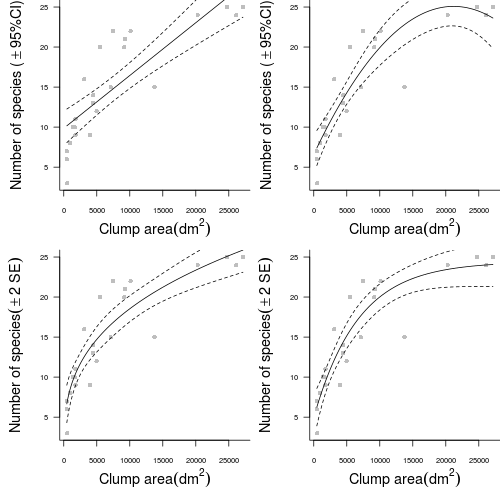
TODO - put in GAM and regression tree examples

Welcome to the end of Workshop 4

  Reading data into R

Ensure that the working directory is pointing to the path containing the file to be imported before proceeding.
To import data into R, we read the contents of a file into a data frame. The general format of the command for reading data into a data frame is

> name <- read.table('filename.csv', header=T, sep=',', row.names=column)

where name is a name you wish the data frame to be referred to as, filename.csv is the name of the csv file that you created in excel and column is the number of the column that had row labels (if there were any). The argument header=T indicates that the variable (vector) names will be created from the names supplied in the first row of the file. The argument sep=',' indicates that entries in the file are separated by a comma (hence a comma delimited file). If the data file does not contain row labels, or you are not sure whether it does, it is best to omit the row.names=column argument.

As an example

> phasmid <- read.data('phasmid.csv', header=T, sep=',', row.names=1)

End of instructions

  Scatterplot matrix (SPLOM)

# make sure the car package is loaded
> library(car)
> scatterplot.matrix(~var1+var2+var3,data=data, diagonal='boxplot')

where var1, var2 etc are the names of numeric vectors in the data data frame (data set)

End of instructions

  Print contents

Predictor variables must not be correlated to the combination of other predictor variables in the fitted model. Multicollinearity has major detrimental effects on model fitting: Multicollinearity can be diagnosed with the following: There are several approaches to dealing with collinearity: Interaction terms in multiplicative models are likely to be correlated to their constituent individual predictors, and thus the partial slopes of these individual predictors are likely to be unstable. However, this problem can be reduced by first centering (subtracting the mean from the predictor values) the individual predictor variables.

End of instructions

  Tolerance and Variance Inflation

The tolerance value for a predictor variable is 1-r2 from the regression of this predictor variable against the other predictor variables included in the linear model. Low tolerances (less than 0.2, approaching 0.1) signify that the predictor value is correlated to the set of other predictor variables (an likely to cause issues).

Variance inflation factor (VIF) is the inverse of tolerance and is just another way of expressing the degree of correlation between a predictor variable and other predictor variables in a linear model. VIF values greater than 5 (approaching 10) indicate strong collinearity and are therefore of concern.

R have a function (vif) for calculating VIF in the car package.

End of instructions

  Multiple linear model fitting

> name.lm <- lm(dv~iv1+iv2, data=data)

where name.lm is a name you provide for the output, dv is the name of the dependent variable and iv1, iv2 etc are the independent variables. data is the name of the data frame (data set).

End of instructions

  Best regression model

Clearly, a regression model that includes all of the predictor variables will explain variation in the response variable better than models containing only a subset of the predictor variables. But how much better? Models with fewer predictor variables are easier and more precise to use for predictive purposes. Moreover, we are most often purely interested in determining which predictors are most important in explaining variation in the response variable.

Therefore, the best regression model should be a model that only includes the most important predictor variables. It should be the most efficient model - that is the model that explains the greatest amount of variation in the response variable with the least number of predictors.

There are a number of ways of determining which model is 'best'. These are based on:
  1. Adjusted r2 - this is the r2 that takes into account the number of predictor variables. It is calculated as the ratio of MSregression/MStotal. Larger values indicate better, more parsimonious models.
  2. AIC - Akaike Information Criterion - based on (log)likelihoods, this is a relative measure of goodness of fit of a model given the set of data. Lower values indicate better, more parsimonious models. The AIC comes in a number of forms;
    • a parametric model only version (extractAIC(model))
    • a generic version (AIC(model))
    • AICc a second order correction (for small sample sizes) version (library(MuMIn);AICc(model))
    • QAIC a quasi-AIC corrected for overdispersion (library(MuMIn);QAIC(model))
  3. BIC - Schwarz Bayesian Information Criterion - is similar to AIC, but it penalizes more heavily against models with more predictors. Lower values indicate better, more parsimonious models. There are two variants on the BIC;
    • a parametric model only version (extractAIC(model,k=log(nrow(dataset))))
    • a generic version (AIC(model,k=log(nrow(dataset))))

End of instructions

  Model selection (dredging) and averaging

Model selection is generally the process of selecting the most parsimonious model from a large collection of possible models. For example, which model explains the most with the fewest predictor variables. For an additive model with five predictor variables, there are large number of possible combinations of predictor variables to assess in order to determine which is the most efficient. There are various techniques that have been used in the past to attempt to find the most efficient models with limited computing power. These techniques (stepwise regression) essentially involve starting with the full saturated model, and incrementally removing the most non-significant term (each time re-running the model) until the model either only contains significant terms or else the goodness of fit measure (adjusted r2) plateaus.

Whilst these techniques were computationally efficient, not all possible combinations of predictor variables were explored. Therefore it is possible that more parsimonious models were overlooked. Recent advances in computing power now permit exploration of all possible model combinations (a process called 'dredging'). Dredging can be performed with one of a number of selection criteria, although AIC, AICc and QAIC are the most popular.

Full exploration (fitting and coefficient estimation) of all possible combinations of predictor terms also allows us to get an estimate of the general effect of any given term across all possible model combinations. This process (called 'model averaging') calculates the average (and confidence intervals) of each regression coefficient across all possible model combinations. Arguably, not only does this provide more accurate estimates, it allows us to estimate the relative contributions (importance) of each predictor term.

Model dredging and averaging in R is a multi-step process - although it can all be done in a single line of code

# make sure the MuMIn package is loaded
> model.avg(get.models(dredge(model, rank = "AIC"),subset=delta<=4))

where model is the fitted model. Working from inside to out (starting with dredge function), all possible combinations of predictors from the original model are explored and the goodness of fit of each is assessed via AIC (the general version). Next the get.models function is used to determine which of all of the models to use in the model averaging process. By default, only those models with a delta (difference in AIC between each model and the model with the lowest AIC) less than or equal to 4 are retained (although this can of course be altered). Finally, this selection of models is used by the model.avg function to calculate the mean (and confidence intervals) regression coefficients and estimate the relative importance of each term. .

End of instructions

  Hierarchical Partitioning

Hierarchical partitioning determines the contributions of individual add joint contributions of each predictor variable by partitioning the r2 for the full model (containing all predictors). The individual contribution of a predictor variable are determined by calculating the improvement in fit (by r2) of a series of models (a hierarchy of models) with and without the predictor variable. Joint contributions are calculated from the differences between partial r2 for a series of models and the independent contributions.

End of instructions

  Hierarchical Partitioning

> loyn2 <- data.frame(logAREA=log10(loyn$AREA), logDIST=log10(loyn$DIST), logLDIST=log10(loyn$LDIST), ALT=loyn$ALT,GRAZE=loyn$GRAZE, YEARS=loyn$YR.ISOL)
> library(Hier.part)
> loyn.hier<-hier.part(loyn$ABUND, loyn2, gof="Rsqu")
> loyn.hier

The first step is to create a data frame that contains only the predictor variables. Then we load a package called hier.part by Chris Walsh and Ralph MacNally (Monash University). This contains the functions necessary to perform hierarchical partitioning in R.
Finally, we use the hier.part() function to perform the hierarchical partitioning and print out the results. The gof= parameter specifies in this case to use r2 values.

End of instructions

  Scatterplots

# load the 'car' library
> library(car)
# generate a scatterplot
> scatterplot(dv~iv,data=data)

where dv is the dependent variable, iv is the independent variable and data is the data frame (data set).

End of instructions

  Linear model fitting

> name.lm <- lm(dv~iv, data=data)

where name.lm is a name you provide for the output, dv is the name of the dependent variable, iv is the name of the independent variable and data is the name of the data frame (data set).

End of instructions

  Linear regression diagnostics

> plot(name.lm)

where name.lm is the name of a fitted linear model. You will be prompted to hit return to cycle through a series of four (or six) diagnostic plots.
  1. The first (and most important of these) is the Residual Plot. The residual plot graphs the residual (differences between observed and expected values) against the fitted (expected) values. Residual plots assist in identifying issues with heterogeneity as well non-linearity
  2. The normal Q-Q plot compares the standardized residuals to normal quantiles. This plot helps identify issues with normality
  3. The scale-location (standardized/normalized residuals) plot, is similar to the residual plot described above except that it is on a standard scale that can permit automatic outlier detection
  4. The Residuals vs Leverage plot. Whilst the residuals are a measure of deviation in y-space, leverage is a measure of deviation in x-space (and thus each is a measure of outlierness). Combined together on this graph, along with Cook's D (measure of outlierness in x/y-shape) contours allows us to identify overly influential observations. Observations approaching the Cook's D contour of 1 are considered highly influential

> resid(name.lm)
> influence.measures(name.lm)

Collectively, these two functions provide information about the relative influence of each observation on the final model fit. Ideally, all observation should have an equal influence on the fit. Outliers are observations that have an over-representative impact on fitted models by pulling trends towards themselves to a greater degree than other observations (and thus biasing outcomes).

The first function lists the residuals corresponding to each of the observation sin the data set (from which the model was fit). A residual measures the difference between an observations observed value and the value that would be expected from the trendline (fitted model). Therefore, the residual value of any observation is a measure of how much of an outlier the observation is in the y-axis direction.

The second function produces a matrix whose rows correspond to each of the observations in the data set (from which the model was fit). The two important columns are the ones labelled 'hat' (the leverage values) and 'cook.d' (Cook's D values). Leverage measures how influential each observation was in the model fit in terms of its deviation in x-space (how unusual is the observation with respect to the other values of the predictor variable?). As with residual values, any leverage values that are much larger than the general set of leverage values should be further explored as they indicate potential outliers. Cook's D combines residual and leverage values into a single value that measures how influential each observation is in both x-space and y-space. As a rule of thumb, Cook's D values approaching 1 should be examined as they are having a larger influence on the model fitting.

End of instructions

  Residual plot

There is a residual for each point. The residuals are the differences between the predicted Y-values (point on the least squares regression line) for each X-value and the observed Y-value for each X-value. A residual plot, plots the residuals (Y-axis) against the predicted Y-values (X-axis) Plot a) shows a uniform spread of data around the least squares regression line and thus there is an even scatter of points in the residual plot (Plot b). In Plot c) the deviations of points from the predicted Y-values become greater with increasing X-values and thus there is a wedge-shape pattern in the residuals. Such a wedge suggests a violation of the homogeneity of variance assumption, and thus the regression may be unreliable.



End of instructions

  Linear relationship vs linear model

Linear models are those statistical models in which a series of parameters (predictor variables) are arranged as a linear combination. That is, within the model, no parameter appears as either a multiplier, divisor or exponent to any other parameter. Importantly, the term 'linear' in this context does not pertain to the nature of the relationship between the response variable and the predictor variable(s), and thus linear models are not restricted to 'linear' (straight-line) relationships. The following examples should help make the distinction.

A linear model representing a linear relationship
A linear model representing a curvilinear relationship
A non-linear model representing a curvilinear relationship

End of instructions

  Fitting Polynomial regression models


> name.lm <- lm(dv~iv+I(iv^2), data=data)

where name.lm is a name you provide for the output, dv is the name of the dependent variable, iv is the name of the independent variable and data is the name of the data frame (data set). The function I() essentially preserves the meaning of the object in brackets so that it treated as a separate term in the model. The above template defines a second order polynomial (quadratic). To define higher order polynomials, add additional instances of the iv to the appropriate power and enclosed within I() functions.

End of instructions


End of instructions

  Testing the null hypothesis that β1=β2=...=0

Testing the null hypothesis that each of the slopes are equal to each other and zero (β1=β2=...=0) is done by comparing the fit of the full model (Y=c+β1X1+β2X2) to the fit of a reduced model that depicts β1 and β2 both equalling zero (ie Y=c).
This specific null hypothesis is summarized when you summarize the linear model fit. It is the F-ratio etc given at the end of the output (highlighted in the picture below).

End of instructions

  Comparing the fit of two models

> anova(reduced.lm, full.lm)

where full.lm is the name of full model and reduced.lm is the name of the reduced model (although it doesn't matter which model is put first - this only effects the sign of some of the resulting values - and you only take absolute values anyway).
A modified ANOVA table will be presented. The bottom line summarizes the results of comparing the two models. This line indicates the F-ratio, degrees of freedom and P-value for the comparison. Note, the F-ratio and P-value obtained from this model comparison is equivelent to the regression coefficient t-value (F=t2) and p-value given in the full model summary.

End of instructions

  Factorial boxplots

> boxplot(dv~factor,data=data)

where dv is the name of the numeric vector (dependent variable), factor is the name of the factor (categorical or factor variable) and data is the name of the data frame (data set). The '~' is used in formulas to represent that the left hand side is proportional to the right hand side.

End of instructions