Jump to main navigation

«
»

Workshop 3 - simple regression

23 April 2011

Basic statistics references

  • Logan (2010) - Chpt 8
  • Quinn & Keough (2002) - Chpt 5
Very basic overview of regression

Simple linear regression

Here is an example from Fowler, Cohen and Parvis (1998). An agriculturalist was interested in the effects of fertilizer load on the yield of grass. Grass seed was sown uniformly over an area and different quantities of commercial fertilizer were applied to each of ten 1 m2 randomly located plots. Two months later the grass from each plot was harvested, dried and weighed. The data are in the file fertilizer.csv.

Download Fertilizer data set

Format of fertilizer.csv data files
FERTILIZERYIELD
2584
5080
7590
100154
125148
......

FERTILIZERMass of fertilizer (g.m-2) - Predictor variable
YIELDYield of grass (g.m-2) - Response variable
turf

Open

Show code

> fert <- read.table("fertilizer.csv", header = T, sep = ",", strip.white = T)

> fert

   FERTILIZER YIELD
1          25    84
2          50    80
3          75    90
4         100   154
5         125   148
6         150   169
7         175   206
8         200   244
9         225   212
10        250   248

the fertilizer data file.
Show code

> fert <- read.table("fertilizer.csv", header = T, sep = ",", strip.white = T)

> fert

   FERTILIZER YIELD
1          25    84
2          50    80
3          75    90
4         100   154
5         125   148
6         150   169
7         175   206
8         200   244
9         225   212
10        250   248

Q1-1. List the following
  1. The biological hypothesis of interest
  2. The biological null hypothesis of interest
  3. The statistical null hypothesis of interest

Q1-2. Test the assumptions of simple linear regression using a scatterplot
of YIELD against FERTILIZER. Add boxplots for each variable to the margins and fit a lowess smoother through the data. Is there any evidence of violations of the simple linear regression assumptions? (Y or N)
Show code

> library(car)

> scatterplot(YIELD ~ FERTILIZER, data = fert)

If there is no evidence that the assumptions of simple linear regression have been violated, fit the linear model
YIELD = intercept + (SLOPE * FERTILIZER). At this stage ignore any output.
Show code

> fert.lm <- lm(YIELD ~ FERTILIZER, data = fert)

Q1-3. Examine the regression diagnostics
(particularly the residual plot
). Does the residual plot indicate any potential problems with the data? (Y or N)
Show code

> par(mfrow = c(2, 3), oma = c(0, 0, 2, 0))

> plot(fert.lm, ask = F, which = 1:6)

> influence.measures(fert.lm)

Influence measures of
 lm(formula = YIELD ~ FERTILIZER, data = fert) :
    dfb.1_ dfb.FERT   dffit cov.r  cook.d   hat inf
1   0.5391  -0.4561  0.5411 1.713 0.15503 0.345    
2  -0.4149   0.3277 -0.4239 1.497 0.09527 0.248    
3  -0.6009   0.4237 -0.6454 0.969 0.18608 0.176    
4   0.3803  -0.2145  0.4634 1.022 0.10137 0.127    
5  -0.0577   0.0163 -0.0949 1.424 0.00509 0.103    
6  -0.0250  -0.0141 -0.0821 1.432 0.00382 0.103    
7   0.0000   0.1159  0.2503 1.329 0.03374 0.127    
8  -0.2193   0.6184  0.9419 0.623 0.31796 0.176    
9   0.3285  -0.6486 -0.8390 1.022 0.30844 0.248    
10  0.1512  -0.2559 -0.3035 1.900 0.05137 0.345   *

Q1-4. If there is no evidence that any of the assumptions have been violated, examine the regression output
. Identify and interpret the following;
Show code

> summary(fert.lm)

Call:
lm(formula = YIELD ~ FERTILIZER, data = fert)
Residuals:
   Min     1Q Median     3Q    Max 
-22.79 -11.07  -5.00  12.00  29.79 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 51.93333   12.97904   4.001  0.00394 ** 
FERTILIZER   0.81139    0.08367   9.697 1.07e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Residual standard error: 19 on 8 degrees of freedom
Multiple R-squared: 0.9216, Adjusted R-squared: 0.9118 
F-statistic: 94.04 on 1 and 8 DF,  p-value: 1.067e-05 

  1. sample y-intercept
  2. sample slope
  3. t value for main H0
  4. R2 value

Q1-5. What conclusions (statistical and biological) would you draw from the analysis?


Q1-6. Significant simple linear regression outcomes are usually accompanied by a scatterpoint that summarizes the relationship between the two population. Construct a scatterplot
without a smoother or marginal boxplots.
Show code

> opar <- par(mar = c(5, 5, 0, 0))

> plot(YIELD ~ FERTILIZER, data = fert, ann = F, axes = F, type = "n")

> points(YIELD ~ FERTILIZER, data = fert, pch = 16)

> axis(1)

> mtext("X-axis label", 1, line = 3)

> axis(2, las = 1)

> mtext("Y-axis label", 2, line = 3)

> box(bty = "l")

> par(opar)


Simple linear regression

Christensen et al. (1996) studied the relationships between coarse woody debris (CWD) and, shoreline vegetation and lake development in a sample of 16 lakes. They defined CWD as debris greater than 5cm in diameter and recorded, for a number of plots on each lake, the basal area (m2.km-1) of CWD in the nearshore water, and the density (no.km-1) of riparian trees along the shore. The data are in the file christ.csv and the relevant variables are the response variable, CWDBASAL (coarse woody debris basal area, m2.km-1), and the predictor variable, RIPDENS (riparian tree density, trees.km-1).

Download Christensen data set

Format of christ.csv data files
LAKERIPDENSCWDBASAL
Bay1270121
Bergner121041
Crampton1800183
Long1875130
Roach1300127
.........

LAKEName of the North American freshwater lake from which the observations were collected
RIPDENSDensity of riparian trees (trees.km-1) Predictor variable
CWDBASALCourse woody debris basal area (m2.km-1) Response variable
Lake

Open the christ data file.
Show code

> christ <- read.table("christ.csv", header = T, sep = ",", strip.white = T)

> head(christ)

        LAKE RIPDENS CWDBASAL
1        Bay    1270      121
2    Bergner    1210       41
3   Crampton    1800      183
4       Long    1875      130
5      Roach    1300      127
6 Tenderfoot    2150      134

Q2-1. List the following
  1. The biological hypothesis of interest
  2. The biological null hypothesis of interest
  3. The statistical null hypothesis of interest

Q2-2. In the table below, list the assumptions of simple linear regression along with how violations of each assumption are diagnosed and/or the risks of violations are minimized.

AssumptionDiagnostic/Risk Minimization
I.
II.
III.
IV.

Q2-3. Draw a scatterplot
of CWDBASAL against RIPDENS. This should include boxplots for each variable to the margins and a fitted lowess smoother through the data HINT.
Show code

> library(car)

> scatterplot(CWDBASAL ~ RIPDENS, data = christ)

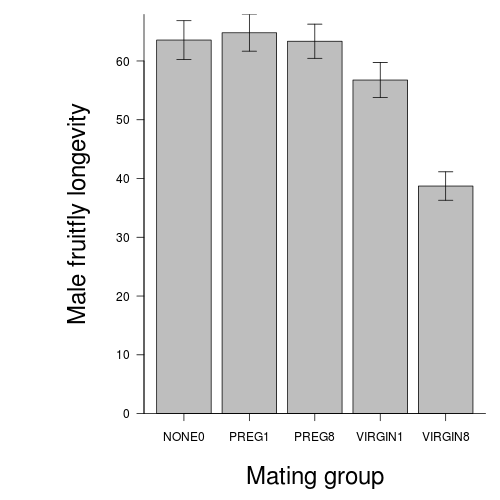
  1. Is there any evidence of nonlinearity? (Y or N)
  2. Is there any evidence of nonnormality? (Y or N)
  3. Is there any evidence of unequal variance? (Y or N)

Q2-4. The main intention of the researchers is to investigate whether there is a linear relationship between the density of riparian vegetation and the size of the logs. They have no of using the model equation for further predictions, not are they particularly interested in the magnitude of the relationship (slope). Is model I or II regression
appropriate in these circumstances?. Explain?

If there is no evidence that the assumptions of simple linear regression have been violated, fit the linear model
CWDBASAL = (SLOPE * RIPDENS) + intercept HINT. At this stage ignore any output.
Show code

> christ.lm <- lm(CWDBASAL ~ RIPDENS, data = christ)

Q2-5. Examine the regression diagnostics
(particularly the residual plot)
HINT. Does the residual plot indicate any potential problems with the data? (Y or N)
Show code

> par(mfrow = c(2, 3), oma = c(0, 0, 2, 0))

> plot(christ.lm, ask = F, which = 1:6)

> influence.measures(christ.lm)

Influence measures of
 lm(formula = CWDBASAL ~ RIPDENS, data = christ) :
     dfb.1_ dfb.RIPD  dffit cov.r  cook.d    hat inf
1   0.09523   0.0230  0.396 0.889 0.07148 0.0627    
2  -0.06051   0.0150 -0.156 1.172 0.01280 0.0631    
3  -0.50292   0.6733  0.822 0.958 0.29787 0.1896    
4   0.10209  -0.1323 -0.155 1.480 0.01293 0.2264   *
5   0.06999   0.0568  0.423 0.857 0.08004 0.0637    
6   0.85160  -1.0289 -1.120 1.482 0.59032 0.4016   *
7  -0.00766  -0.0175 -0.084 1.222 0.00377 0.0653    
8   0.13079  -0.0961  0.163 1.235 0.01401 0.0959    
9  -0.16369   0.1207 -0.203 1.211 0.02156 0.0967    
10  0.02294  -0.1138 -0.311 1.042 0.04742 0.0722    
11 -0.02588  -0.0101 -0.120 1.198 0.00763 0.0629    
12  0.49223  -0.3571  0.622 0.769 0.16169 0.0932    
13 -0.12739   0.1065 -0.137 1.355 0.01007 0.1570    
14 -0.15382   0.1248 -0.171 1.301 0.01550 0.1340    
15 -0.21860   0.1721 -0.251 1.224 0.03278 0.1178    
16 -0.22479   0.1666 -0.277 1.156 0.03922 0.0979    

Q2-6. At this point, we have no evidence to suggest that the hypothesis tests will not be reliable. Examine the regression output and identify and interpret the following:
Show code

> summary(christ.lm)

Call:
lm(formula = CWDBASAL ~ RIPDENS, data = christ)
Residuals:
   Min     1Q Median     3Q    Max 
-38.62 -22.41 -13.33  26.16  61.35 
Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -77.09908   30.60801  -2.519 0.024552 *  
RIPDENS       0.11552    0.02343   4.930 0.000222 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Residual standard error: 36.32 on 14 degrees of freedom
Multiple R-squared: 0.6345, Adjusted R-squared: 0.6084 
F-statistic:  24.3 on 1 and 14 DF,  p-value: 0.0002216 

  1. sample y-intercept
  2. sample slope
  3. t value for main H0
  4. P-value for main H0
  5. R2 value

Q2-7. What conclusions (statistical and biological) would you draw from the analysis?

Simple linear regression

Here is a modified example from Quinn and Keough (2002). Peake & Quinn (1993) investigated the relationship between the number of individuals of invertebrates living in amongst clumps of mussels on a rocky intertidal shore and the area of those mussel clumps.

Download PeakeQuinn data set

Format of peakquinn.csv data files
AREAINDIV
516.0018
469.0660
462.2557
938.60100
1357.1548
......

AREAArea of mussel clump mm2 - Predictor variable
INDIVNumber of individuals found within clump - Response variable
clump of mussels

Open the peakquinn data file.
Show code

> peakquinn <- read.table("peakquinn.csv", header = T, sep = ",",

> strip.white = T)

> peakquinn

     AREA INDIV
1  516.00    18
2  469.06    60
3  462.25    57
4  938.60   100
5 1357.15    48
6 1773.66   118

The relationship between two continuous variables can be analyzed by simple linear regression. As with question 2, note that the levels of the predictor variable were measured, not fixed, and thus parameter estimates should be based on model II RMA regression. Note however, that the hypothesis test for slope is uneffected by whether the predictor variable is fixed or measured.

Before performing the analysis we need to check the assumptions. To evaluate the assumptions of linearity, normality and homogeneity of variance, construct a scatterplot
of INDIV against AREA (INDIV on y-axis, AREA on x-axis) including a lowess smoother and boxplots on the axes.
Show code

> library(car)

> scatterplot(INDIV ~ AREA, data = peakquinn)

Q3-1. Consider the assumptions and suitability of the data for simple linear regression:
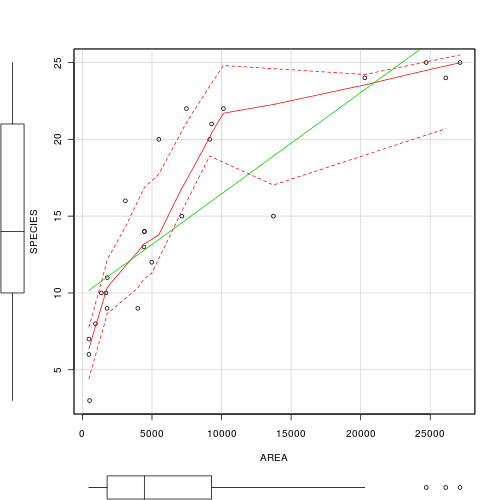
  1. In this case, the researchers are interested in investigating whether there is a relationship between the number of invertebrate individuals and mussel clump area as well as generating a predictive model. However, they are not interested in the specific magnitude of the relationship (slope) and have no intension of comparing their slope to any other non-zero values. Is model I or II regression
    appropriate in these circumstances?. Explain?
  2. Is there any evidence that the other assumptions are likely to be violated?

To get an appreciation of what a residual plot would look like when there is some evidence that the assumption of homogeneity of variance assumption has been violated, perform the simple linear regression (by fitting a linear model)
Show code

> peakquinn.lm <- lm(INDIV ~ AREA, data = peakquinn)

purely for the purpose of examining the regression diagnostics
(particularly the residual plot)
Show code

> par(mfrow = c(2, 3), oma = c(0, 0, 2, 0))

> plot(peakquinn.lm, ask = F, which = 1:6)

> influence.measures(peakquinn.lm)

Influence measures of
 lm(formula = INDIV ~ AREA, data = peakquinn) :
    dfb.1_ dfb.AREA    dffit cov.r   cook.d    hat inf
1  -0.1999  0.13380 -0.20006 1.125 2.04e-02 0.0724    
2  -0.1472  0.09887 -0.14731 1.150 1.12e-02 0.0728    
3  -0.1507  0.10121 -0.15073 1.148 1.17e-02 0.0728    
4  -0.1153  0.07466 -0.11549 1.155 6.92e-03 0.0687    
5  -0.1881  0.11765 -0.18896 1.117 1.82e-02 0.0653    
6  -0.1214  0.07306 -0.12237 1.142 7.75e-03 0.0622    
7  -0.0858  0.05206 -0.08639 1.155 3.88e-03 0.0628    
8  -0.0176  0.01059 -0.01776 1.165 1.65e-04 0.0621    
9  -0.0509  0.02633 -0.05236 1.150 1.43e-03 0.0535    
10 -0.0237  0.01069 -0.02504 1.148 3.28e-04 0.0489    
11  0.0475 -0.01961  0.05096 1.141 1.35e-03 0.0470    
12 -0.0418  0.01717 -0.04492 1.142 1.05e-03 0.0468    
13 -0.0061  0.00221 -0.00672 1.144 2.36e-05 0.0448    
14 -0.0453  0.01859 -0.04862 1.142 1.23e-03 0.0468    
15  0.1641 -0.05100  0.18584 1.067 1.74e-02 0.0433    
16  0.0472 -0.00254  0.06317 1.129 2.08e-03 0.0401    
17  0.1764 -0.01859  0.22781 1.021 2.57e-02 0.0403    
18  0.0542  0.01493  0.09093 1.120 4.28e-03 0.0411    
19  0.2173  0.12011  0.43430 0.808 8.29e-02 0.0433    
20 -0.0701 -0.02168 -0.12016 1.106 7.43e-03 0.0413    
21  0.1849  0.63635  1.07759 0.357 3.36e-01 0.0614   *
22  0.0752 -0.33126 -0.39474 1.157 7.79e-02 0.1352    
23 -0.0789  0.22611  0.25071 1.362 3.25e-02 0.2144   *
24  0.0853 -0.21744 -0.23573 1.473 2.88e-02 0.2681   *
25  0.4958 -1.32133 -1.44477 0.865 8.44e-01 0.2445   *

Q3-2. How would you describe the residual plot?

Q3-3. What could be done to the data to address the problems highlighted by the scatterplot, boxplots and residuals?

Q3-4. Describe how the scatterplot, axial boxplots and residual plot might appear following successful data transformation.

Transform
both variables to logs (base 10), replot the scatterplot using the transformed data, refit the linear model (again using transformed data) and examine the residual plot.HINT
Show code

> library(car)

> scatterplot(log10(INDIV) ~ log10(AREA), data = peakquinn)

Q3-5. Would you consider the transformation as successful? (Y or N)

Q3-6. If you are satisfied that the assumptions of the analysis are likely to have been met, perform the linear regression analysis (refit the linear model) HINT, examine the output.
Show code

> peakquinn.lm <- lm(log10(INDIV) ~ log10(AREA), data = peakquinn)

> par(mfrow = c(2, 3), oma = c(0, 0, 2, 0))

> plot(fert.lm, ask = F, which = 1:6)

> summary(peakquinn.lm)

Call:
lm(formula = log10(INDIV) ~ log10(AREA), data = peakquinn)
Residuals:
     Min       1Q   Median       3Q      Max 
-0.43355 -0.06464  0.02219  0.11178  0.26818 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.57601    0.25904  -2.224   0.0363 *  
log10(AREA)  0.83492    0.07066  11.816 3.01e-11 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Residual standard error: 0.1856 on 23 degrees of freedom
Multiple R-squared: 0.8586, Adjusted R-squared: 0.8524 
F-statistic: 139.6 on 1 and 23 DF,  p-value: 3.007e-11 

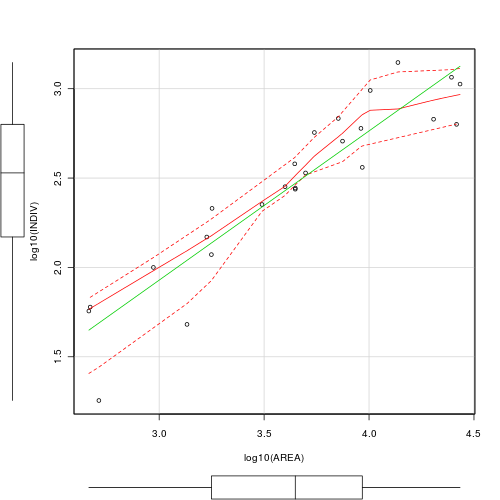
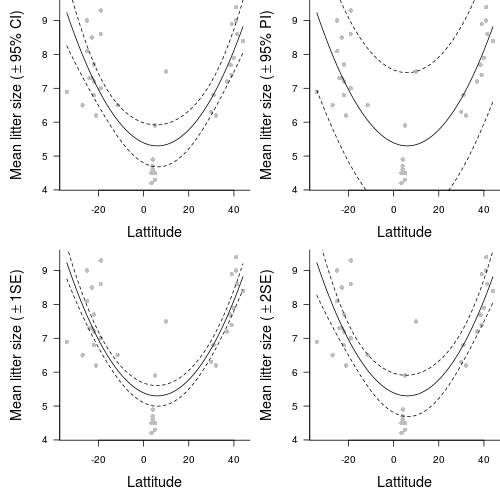
  1. Test the null hypothesis that the population slope of the regression line between log number of individuals and log clump area is zero - use either the t-test or ANOVA F-test regression output. What are your conclusions (statistical and biological)? HINT
  2. If the relationship is significant construct the regression equation relating the number of individuals in the a clump to the clump size. Remember that parameter estimates should be based on RMA regression not OLS!
    DV=intercept+slopexIV
    Log10Individuals Log10Area

Q3-7. Write the results out as though you were writing a research paper/thesis. For example (select the phrase that applies and fill in gaps with your results): 
A linear regression of log number of individuals against log clump area showed (choose correct option)
(b = , t = , df = , P = )

Q3-8. How much of the variation in log individual number is explained by the linear relationship with log clump area? That is , what is the R2 value?

Q3-9. What number of individuals would you predict
for a new clump with an area of 8000 mm2? HINT
Show code

> 10^predict(peakquinn.lm, newdata = data.frame(AREA = 8000), interval = "predict")

       fit      lwr      upr
1 481.6561 194.5975 1192.167

> 10^predict(peakquinn.lm, newdata = data.frame(AREA = 8000), interval = "confidence")

       fit      lwr      upr
1 481.6561 394.5162 588.0434

Q3-10. Given that in this case both response and predictor variables were measured (the levels of the predictor variable were not specifically set by the researchers), it might be worth presenting the less biased model parameters (y-intercept and slope) from RMA model II regression. Perform the RMA model II regression
and examine the slope and intercept
  1. b (slope):
  2. c (y-intercept):

Q3-11. Significant simple linear regression outcomes are usually accompanied by a scatterpoint that summarizes the relationship between the two population. Construct a scatterplot
without a smoother or marginal boxplots. Consider whether or not transformed or untransformed data should be used in this graph.
Show code

> opar <- par(mar = c(6, 6, 0, 0))

> plot(INDIV ~ AREA, data = peakquinn, log = "xy", ann = F, axes = F,

> type = "n")

> points(INDIV ~ AREA, data = peakquinn, pch = 16)

> axis(1)

> mtext(expression(paste("Mussel clump area ", (mm^2))), 1, line = 4,

> cex = 2)

> axis(2, las = 1)

> mtext("Number of individuals per clump", 2, line = 4, cex = 2)

> xs <- seq(min(peakquinn$AREA), max(peakquinn$AREA), l = 1000)

> ys <- 10^predict(peakquinn.lm, newdata = data.frame(AREA = xs),

> interval = "c")

> lines(ys[, "fit"] ~ xs)

> matlines(xs, ys, lty = 2, col = 1)

> text(max(peakquinn$AREA), 20, expression(paste(log[10], "INDIV = 0.835.",

> log[10], "AREA - 0.576")), pos = 2)

> text(max(peakquinn$AREA), 17, expression(paste(R^2 == 0.857)),

> pos = 2)

> box(bty = "l")

> par(opar)


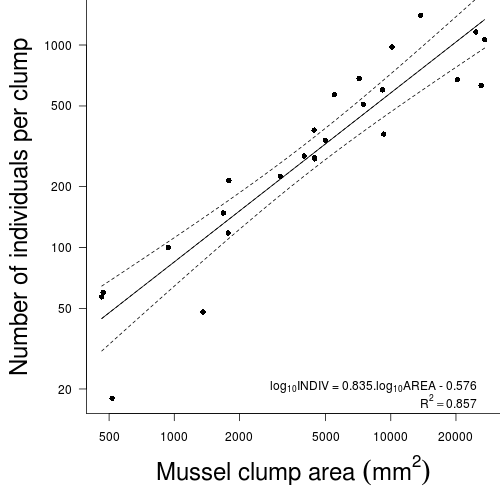
Model II RMA regression

Nagy, Girard & Brown (1999) investigated the allometric scaling relationships for mammals (79 species), reptiles (55 species) and birds (95 species). The observed relationships between body size and metabolic rates of organisms have attracted a great deal of discussion amongst scientists from a wide range of disciplines recently. Whilst some have sort to explore explanations for the apparently 'universal' patterns, Nagy et al. (1999) were interested in determining whether scaling relationships differed between taxonomic, dietary and habitat groupings.

Download Nagy data set

Format of nagy.csv data file
SpeciesCommonMassFMRTaxonHabitatDietClass
Pipistrellus pipistrellusPipistrelle7.329.3ChNDIMammal
Plecotus auritus Brown long-eared bat 8.5 27.6 Ch ND I Mammal
Myotis lucifugus Little brown bat 9.0 29.9 Ch ND I Mammal
Gerbillus henleyi Northern pygmy gerbil 9.3 26.5 Ro D G Mammal
Tarsipes rostratus Honey possum 9.9 34.4 Tr ND N Mammal
................

Open the nagy data file.
Show code

> nagy <- read.table("nagy.csv", header = T, sep = ",", strip.white = T)

> head(nagy)

                    Species                Common Mass  FMR Taxon Habitat Diet
1 Pipistrellus pipistrellus           Pipistrelle  7.3 29.3    Ch      ND    I
2          Plecotus auritus  Brown long-eared bat  8.5 27.6    Ch      ND    I
3          Myotis lucifugus      Little brown bat  9.0 29.9    Ch      ND    I
4         Gerbillus henleyi Northern pygmy gerbil  9.3 26.5    Ro       D    G
5        Tarsipes rostratus          Honey possum  9.9 34.4    Tr      ND    N
6           Anoura caudifer   Flower-visiting bat 11.5 51.9    Ch      ND    N
   Class   MASS
1 Mammal 0.0073
2 Mammal 0.0085
3 Mammal 0.0090
4 Mammal 0.0093
5 Mammal 0.0099
6 Mammal 0.0115

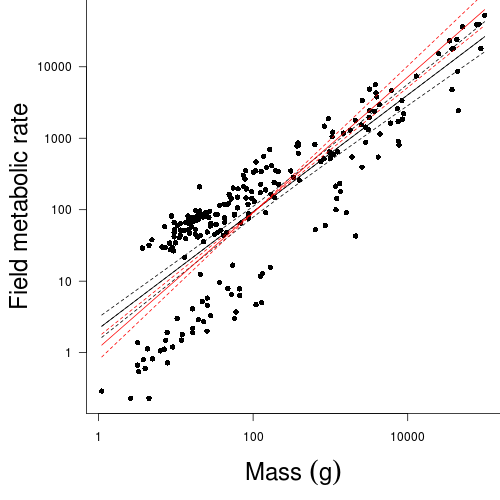
For this example, we will explore the relationships between field metabolic rate (FMR) and body mass (Mass) in grams for the entire data set and then separately for each of the three classes (mammals, reptiles and aves).

Unlike the previous examples in which both predictor and response variables could be considered 'random' (measured not set), parameter estimates should be based on model II RMA regression. However, unlike previous examples, in this example, the primary focus is not hypothesis testing about whether there is a relationship or not. Nor is prediction a consideration. Instead, the researchers are interested in establishing (and comparing) the allometric scaling factors (slopes) of the metabolic rate - body mass relationships. Hence in this case, model II regression is indeed appropriate.

Q4-1. Before performing the analysis we need to check the assumptions. To evaluate the assumptions of linearity, normality and homogeneity of variance, construct a scatterplot
of FMR against Mass including a lowess smoother and boxplots on the axes.
Show code

> library(car)

> scatterplot(FMR ~ Mass, data = nagy)

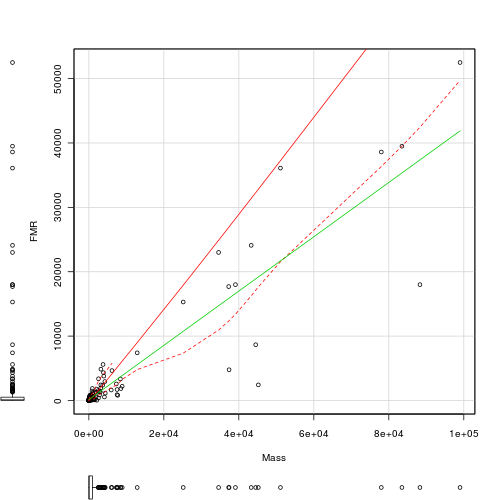
  1. Is there any evidence of non-normality?
  2. Is there any evidence of non-linearity?

Q4-2. Typically, allometric scaling data are treated by a log-log transformation. That is, both predictor and response variables are log10 transformed. This is achieved graphically on a scatterplot by plotting the data on log transformed axes. Produce such a scatterplot (HINT). Does this improve linearity?
Show code

> library(car)

> scatterplot(FMR ~ Mass, data = nagy, log = "xy")

Q4-3. Fit the linear models relating log-log transformed FMR and Mass using both the Ordinary Least Squares and Reduced Major Axis methods separately for each of the classes (mammals, reptiles and aves).
Show code

> nagy.olsM <- lm(log10(FMR) ~ log10(Mass), data = subset(nagy,

> nagy$Class == "Mammal"))

> summary(nagy.olsM)

Call:
lm(formula = log10(FMR) ~ log10(Mass), data = subset(nagy, nagy$Class == 
    "Mammal"))
Residuals:
     Min       1Q   Median       3Q      Max 
-0.60271 -0.13172 -0.00811  0.14440  0.41794 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.68301    0.05336   12.80   <2e-16 ***
log10(Mass)  0.73412    0.01924   38.15   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Residual standard error: 0.2119 on 77 degrees of freedom
Multiple R-squared: 0.9498, Adjusted R-squared: 0.9491 
F-statistic:  1456 on 1 and 77 DF,  p-value: < 2.2e-16 

> nagy.olsR <- lm(log10(FMR) ~ log10(Mass), data = subset(nagy,

> nagy$Class == "Reptiles"))

> summary(nagy.olsR)

Call:
lm(formula = log10(FMR) ~ log10(Mass), data = subset(nagy, nagy$Class == 
    "Reptiles"))
Residuals:
     Min       1Q   Median       3Q      Max 
-0.61438 -0.07813 -0.00782  0.17257  0.39794 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.70658    0.05941  -11.89   <2e-16 ***
log10(Mass)  0.88789    0.02941   30.19   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Residual standard error: 0.2289 on 53 degrees of freedom
Multiple R-squared: 0.945, Adjusted R-squared: 0.944 
F-statistic: 911.5 on 1 and 53 DF,  p-value: < 2.2e-16 

> nagy.olsA <- lm(log10(FMR) ~ log10(Mass), data = subset(nagy,

> nagy$Class == "Aves"))

> summary(nagy.olsA)

Call:
lm(formula = log10(FMR) ~ log10(Mass), data = subset(nagy, nagy$Class == 
    "Aves"))
Residuals:
     Min       1Q   Median       3Q      Max 
-0.53281 -0.07884  0.00453  0.09973  0.41202 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.01945    0.03929   25.95   <2e-16 ***
log10(Mass)  0.68079    0.01817   37.46   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
Residual standard error: 0.1653 on 93 degrees of freedom
Multiple R-squared: 0.9378, Adjusted R-squared: 0.9372 
F-statistic:  1403 on 1 and 93 DF,  p-value: < 2.2e-16 

> library(lmodel2)

> nagy.rmaM <- lmodel2(log10(FMR) ~ log10(Mass), data = subset(nagy,

> nagy$Class == "Mammal"), nperm = 99, range.y = "interval",

> range.x = "interval")

> nagy.rmaM

Model II regression
Call: lmodel2(formula = log10(FMR) ~ log10(Mass), data = subset(nagy,
nagy$Class == "Mammal"), range.y = "interval", range.x = "interval",
nperm = 99)
n = 79   r = 0.9745562   r-square = 0.9497597 
Parametric P-values:   2-tailed = 9.0925e-52    1-tailed = 4.54625e-52 
Angle between the two OLS regression lines = 1.419216 degrees
Permutation tests of OLS, MA, RMA slopes: 1-tailed, tail corresponding to sign
A permutation test of r is equivalent to a permutation test of the OLS slope
P-perm for SMA = NA because the SMA slope cannot be tested
Regression results
  Method Intercept     Slope  Angle (degrees)  P-perm (1-tailed)
1    OLS 0.6830113 0.7341230         36.28325               0.01
2     MA 0.6488611 0.7478872         36.79234               0.01
3    SMA 0.6354571 0.7532896         36.99033                 NA
4    RMA 0.6427932 0.7503328         36.88210               0.01
Confidence intervals
  Method  2.5%-Intercept 97.5%-Intercept  2.5%-Slope 97.5%-Slope
1    OLS       0.5767519       0.7892707   0.6958080   0.7724381
2     MA       0.5501362       0.7439564   0.7095593   0.7876780
3    SMA       0.5379776       0.7281045   0.7159483   0.7925784
4    RMA       0.5434049       0.7378891   0.7120047   0.7903910
Eigenvalues: 2.408867 0.02861954 
H statistic used for computing C.I. of MA: 0.0006266053 

> library(lmodel2)

> nagy.rmaR <- lmodel2(log10(FMR) ~ log10(Mass), data = subset(nagy,

> nagy$Class == "Reptiles"), nperm = 99, range.y = "interval",

> range.x = "interval")

> nagy.rmaR

Model II regression
Call: lmodel2(formula = log10(FMR) ~ log10(Mass), data = subset(nagy,
nagy$Class == "Reptiles"), range.y = "interval", range.x = "interval",
nperm = 99)
n = 55   r = 0.9721361   r-square = 0.9450487 
Parametric P-values:   2-tailed = 4.560243e-35    1-tailed = 2.280121e-35 
Angle between the two OLS regression lines = 1.612304 degrees
Permutation tests of OLS, MA, RMA slopes: 1-tailed, tail corresponding to sign
A permutation test of r is equivalent to a permutation test of the OLS slope
P-perm for SMA = NA because the SMA slope cannot be tested
Regression results
  Method  Intercept     Slope  Angle (degrees)  P-perm (1-tailed)
1    OLS -0.7065753 0.8878871         41.60146               0.01
2     MA -0.7464273 0.9109729         42.33267               0.01
3    SMA -0.7505069 0.9133362         42.40658                 NA
4    RMA -0.7525920 0.9145440         42.44429               0.01
Confidence intervals
  Method  2.5%-Intercept 97.5%-Intercept  2.5%-Slope 97.5%-Slope
1    OLS      -0.8257399      -0.5874106   0.8288999   0.9468743
2     MA      -0.8542083      -0.6449544   0.8521909   0.9734091
3    SMA      -0.8556188      -0.6519646   0.8562518   0.9742262
4    RMA      -0.8613191      -0.6511803   0.8557975   0.9775283
Eigenvalues: 2.028696 0.02842206 
H statistic used for computing C.I. of MA: 0.00109388 

> library(lmodel2)

> nagy.rmaA <- lmodel2(log10(FMR) ~ log10(Mass), data = subset(nagy,

> nagy$Class == "Aves"), nperm = 99, range.y = "interval",

> range.x = "interval")

> nagy.rmaA

Model II regression
Call: lmodel2(formula = log10(FMR) ~ log10(Mass), data = subset(nagy,
nagy$Class == "Aves"), range.y = "interval", range.x = "interval",
nperm = 99)
n = 95   r = 0.9684215   r-square = 0.9378401 
Parametric P-values:   2-tailed = 6.735679e-58    1-tailed = 3.36784e-58 
Angle between the two OLS regression lines = 1.72973 degrees
Permutation tests of OLS, MA, RMA slopes: 1-tailed, tail corresponding to sign
A permutation test of r is equivalent to a permutation test of the OLS slope
P-perm for SMA = NA because the SMA slope cannot be tested
Regression results
  Method Intercept     Slope  Angle (degrees)  P-perm (1-tailed)
1    OLS 1.0194531 0.6807916         34.24670               0.01
2     MA 0.9911840 0.6952883         34.81044               0.01
3    SMA 0.9761635 0.7029910         35.10687                 NA
4    RMA 0.9718087 0.7052242         35.19242               0.01
Confidence intervals
  Method  2.5%-Intercept 97.5%-Intercept  2.5%-Slope 97.5%-Slope
1    OLS       0.9414302        1.097476   0.6447005   0.7168826
2     MA       0.9180201        1.061862   0.6590437   0.7328076
3    SMA       0.9039794        1.044737   0.6678258   0.7400078
4    RMA       0.8966869        1.042671   0.6688852   0.7437475
Eigenvalues: 1.296792 0.01835144 
H statistic used for computing C.I. of MA: 0.0006174023 


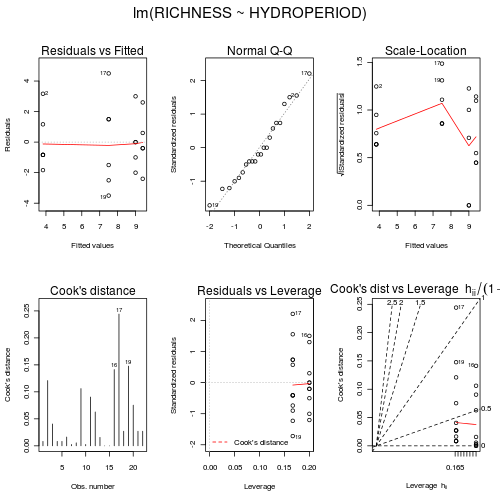
Indicate the following;
 OLSRMA 
ClassSlopeInterceptSlopeInterceptR2
Mammals (HINT and HINT)
Reptiles (HINT and HINT)
Aves (HINT and HINT)

Q4-4. Produce a scatterplot that depicts the relationship between FMR and Mass just for the mammals (HINT)
  1. Fit the OLS regression line to this plot (HINT)
  2. Fit the RMA regression line (in red) to this plot (HINT)
Show code

> opar <- par(mar = c(6, 6, 0, 0))

> plot(FMR ~ Mass, data = subset(nagy, nagy$Class == "Mammal"),

> log = "xy", ann = F, axes = F, type = "n")

> points(FMR ~ Mass, data = subset(nagy, nagy$Class == "Mammal"),

> pch = 16)

> axis(1)

> mtext(expression(paste("Mass ", (g))), 1, line = 4, cex = 2)

> axis(2, las = 1)

> mtext("Field metabolic rate", 2, line = 4, cex = 2)

> xs <- with(subset(nagy, nagy$Class == "Mammal"), seq(min(Mass),

> max(Mass), l = 1000))

> ys <- 10^predict(nagy.olsM, newdata = data.frame(Mass = xs),

> interval = "c")

> lines(ys[, "fit"] ~ xs)

> matlines(xs, ys, lty = 2, col = 1)

> centr.y <- mean(nagy.rmaM$y)

> centr.x <- mean(nagy.rmaM$x)

> A <- nagy.rmaM$regression.results[4, 2]

> B <- nagy.rmaM$regression.results[4, 3]

> B1 <- nagy.rmaM$confidence.intervals[4, 4]

> A1 <- centr.y - B1 * centr.x

> B2 <- nagy.rmaM$confidence.intervals[4, 5]

> A2 <- centr.y - B2 * centr.x

> lines(10^(A + (log10(xs) * B)) ~ xs, col = "red")

> lines(10^(A1 + (log10(xs) * B1)) ~ xs, col = "red", lty = 2)

> lines(10^(A2 + (log10(xs) * B2)) ~ xs, col = "red", lty = 2)

> box(bty = "l")

> par(opar)

Q4-5. Compare and contrast the OLS and RMA parameter estimates. Explain which estimates are most appropriate and why the in this case the two methods produce very similar estimates.

Q4-6. To see how the degree of correlation can impact on the difference between OLS and RMA estimates, fit the relationship between FMR and Mass for the entire data set.
Show code

> library(lmodel2)

> nagy.rma <- lmodel2(log10(FMR) ~ log10(Mass), data = nagy, nperm = 99,

> range.y = "interval", range.x = "interval")

> nagy.rma

Model II regression
Call: lmodel2(formula = log10(FMR) ~ log10(Mass), data = nagy, range.y
= "interval", range.x = "interval", nperm = 99)
n = 229   r = 0.8455446   r-square = 0.7149457 
Parametric P-values:   2-tailed = 8.508257e-64    1-tailed = 4.254129e-64 
Angle between the two OLS regression lines = 9.562711 degrees
Permutation tests of OLS, MA, RMA slopes: 1-tailed, tail corresponding to sign
A permutation test of r is equivalent to a permutation test of the OLS slope
P-perm for SMA = NA because the SMA slope cannot be tested
Regression results
  Method  Intercept     Slope  Angle (degrees)  P-perm (1-tailed)
1    OLS 0.33568100 0.8176849         39.27235               0.01
2     MA 0.03733871 0.9611536         43.86524               0.01
3    SMA 0.02507474 0.9670512         44.04036                 NA
4    RMA 0.06555885 0.9475829         43.45832               0.01
Confidence intervals
  Method  2.5%-Intercept 97.5%-Intercept  2.5%-Slope 97.5%-Slope
1    OLS       0.1762815       0.4950805   0.7501591   0.8852108
2     MA      -0.1346868       0.1962303   0.8847449   1.0438783
3    SMA      -0.1202414       0.1605978   0.9018800   1.0369317
4    RMA      -0.1033674       0.2227793   0.8719778   1.0288172
Eigenvalues: 2.238598 0.1871019 
H statistic used for computing C.I. of MA: 0.001702262 

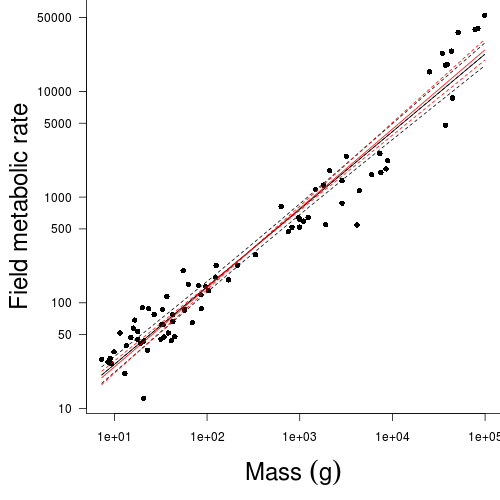
  1. Complete the following table
     OLSRMA 
    ClassSlopeInterceptSlopeInterceptR2
    Entire data set (HINT and HINT)
  2. Produce a scatterplot that depicts the relationship between FMR and Mass for the entire data set (HINT)
  3. Fit the OLS regression line to this plot (HINT)
  4. Fit the RMA regression line (in red) to this plot (HINT)
  5. Compare and contrast the OLS and RMA parameter estimates. Explain which estimates are most appropriate and why the in this case the two methods produce not so similar estimates.
Show code

> opar <- par(mar = c(6, 6, 0, 0))

> plot(FMR ~ Mass, data = nagy, log = "xy", ann = F, axes = F,

> type = "n")

> points(FMR ~ Mass, data = nagy, pch = 16)

> axis(1)

> mtext(expression(paste("Mass ", (g))), 1, line = 4, cex = 2)

> axis(2, las = 1)

> mtext("Field metabolic rate", 2, line = 4, cex = 2)

> xs <- with(nagy, seq(min(Mass), max(Mass), l = 1000))

> nagy.lm <- lm(log10(FMR) ~ log10(Mass), data = nagy)

> ys <- 10^predict(nagy.lm, newdata = data.frame(Mass = xs), interval = "c")

> lines(ys[, "fit"] ~ xs)

> matlines(xs, ys, lty = 2, col = 1)

> centr.y <- mean(nagy.rma$y)

> centr.x <- mean(nagy.rma$x)

> A <- nagy.rma$regression.results[4, 2]

> B <- nagy.rma$regression.results[4, 3]

> B1 <- nagy.rma$confidence.intervals[4, 4]

> A1 <- centr.y - B1 * centr.x

> B2 <- nagy.rma$confidence.intervals[4, 5]

> A2 <- centr.y - B2 * centr.x

> lines(10^(A + (log10(xs) * B)) ~ xs, col = "red")

> lines(10^(A1 + (log10(xs) * B1)) ~ xs, col = "red", lty = 2)

> lines(10^(A2 + (log10(xs) * B2)) ~ xs, col = "red", lty = 2)

> box(bty = "l")

> par(opar)

Welcome to the end of Workshop 3

  Reading data into R

Ensure that the working directory is pointing to the path containing the file to be imported before proceeding.
To import data into R, we read the contents of a file into a data frame. The general format of the command for reading data into a data frame is

> name <- read.table('filename.csv', header=T, sep=',', row.names=column, strip.white=T)

where name is a name you wish the data frame to be referred to as, filename.csv is the name of the csv file that you created in excel and column is the number of the column that had row labels (if there were any). The argument header=T indicates that the variable (vector) names will be created from the names supplied in the first row of the file. The argument sep=',' indicates that entries in the file are separated by a comma (hence a comma delimited file). If the data file does not contain row labels, or you are not sure whether it does, it is best to omit the row.names=column argument. The strip.white=T arguement ensures that no leading or trailing spaces are left in character names (these can be particularly nasty in categorical variables!).

As an example

> phasmid <- read.data("phasmid.csv", header = T, sep = ",", row.names = 1,

> strip.white = T)

End of instructions

  Scatterplots

# load the 'car' library
> library(car)
# generate a scatterplot
> scatterplot(dv~iv,data=data)

where dv is the dependent variable, iv is the independent variable and data is the data frame (data set).

End of instructions

  Linear model fitting

> name.lm <- lm(dv~iv, data=data)

where name.lm is a name you provide for the output, dv is the name of the dependent variable, iv is the name of the independent variable and data is the name of the data frame (data set).

End of instructions

  Linear regression diagnostics

> plot(name.lm)

where name.lm is the name of a fitted linear model. You will be prompted to hit return to cycle through a series of four (or six) diagnostic plots.
  1. The first (and most important of these) is the Residual Plot. The residual plot graphs the residual (differences between observed and expected values) against the fitted (expected) values. Residual plots assist in identifying issues with heterogeneity as well non-linearity
  2. The normal Q-Q plot compares the standardized residuals to normal quantiles. This plot helps identify issues with normality
  3. The scale-location (standardized/normalized residuals) plot, is similar to the residual plot described above except that it is on a standard scale that can permit automatic outlier detection
  4. The Residuals vs Leverage plot. Whilst the residuals are a measure of deviation in y-space, leverage is a measure of deviation in x-space (and thus each is a measure of outlierness). Combined together on this graph, along with Cook's D (measure of outlierness in x/y-shape) contours allows us to identify overly influential observations. Observations approaching the Cook's D contour of 1 are considered highly influential

> resid(name.lm)
> influence.measures(name.lm)

Collectively, these two functions provide information about the relative influence of each observation on the final model fit. Ideally, all observation should have an equal influence on the fit. Outliers are observations that have an over-representative impact on fitted models by pulling trends towards themselves to a greater degree than other observations (and thus biasing outcomes).

The first function lists the residuals corresponding to each of the observation sin the data set (from which the model was fit). A residual measures the difference between an observations observed value and the value that would be expected from the trendline (fitted model). Therefore, the residual value of any observation is a measure of how much of an outlier the observation is in the y-axis direction.

The second function produces a matrix whose rows correspond to each of the observations in the data set (from which the model was fit). The two important columns are the ones labelled 'hat' (the leverage values) and 'cook.d' (Cook's D values). Leverage measures how influential each observation was in the model fit in terms of its deviation in x-space (how unusual is the observation with respect to the other values of the predictor variable?). As with residual values, any leverage values that are much larger than the general set of leverage values should be further explored as they indicate potential outliers. Cook's D combines residual and leverage values into a single value that measures how influential each observation is in both x-space and y-space. As a rule of thumb, Cook's D values approaching 1 should be examined as they are having a larger influence on the model fitting.

End of instructions

  Residual plot

There is a residual for each point. The residuals are the differences between the predicted Y-values (point on the least squares regression line) for each X-value and the observed Y-value for each X-value. A residual plot, plots the residuals (Y-axis) against the predicted Y-values (X-axis) Plot a) shows a uniform spread of data around the least squares regression line and thus there is an even scatter of points in the residual plot (Plot b). In Plot c) the deviations of points from the predicted Y-values become greater with increasing X-values and thus there is a wedge-shape pattern in the residuals. Such a wedge suggests a violation of the homogeneity of variance assumption, and thus the regression may be unreliable.



End of instructions

  Regression output

#print a summary of the linear model coefficients
> summary(name.lm)
#print a summary of the ANOVA table
> anova(name.lm)

where name.lm is the name of a fitted linear model.

End of instructions

  Scatterplots

# construct the base plot without axes or labels or even points
> plot(dv~iv,data=data, ann=F, axes=F, type="n")
# put the points on as solid circles (point character 16)
> points(dv~iv,data=data, pch=16)
# draw the x-axis
> axis(1)
> mtext("X-axis label",1)
# draw the y-axis (labels rotated)
> axis(2,las=1)
> mtext("Y-axis label",2)
#put an 'L'-shaped box around the plot
> box(bty="l")

where dv is the dependent variable, iv is the independent variable and data is the data frame (data set).

End of instructions

  EDA - Linearity

The most common methods for analysing the relationship or association between variables.assume that the variables are linearly related (or more correctly, that they do not covary according to some function other than linear). For example, to examine for the presence and strength of the relationship between two variables (such as those depicted below), it is a requirement of the more basic statistical tests that the variables not be related by any function other than a linear (straight line) function if any function at all.

There is no evidence that the data represented in Figure (a) are related (covary) according to any function other than linear. Likewise, there is no evidence that the data represented in Figure (b) are related (covary) according to any function other than linear (if at all). However, there is strong evidence that the data represented in Figure (c) are not related linearly. Hence Figure (c) depicts evidence for a violation in the statistical necessity of linearity.

End of instructions

  EDA - Normal distribution

Parametric statistical hypothesis tests assume that the population measurements follow a specific distribution. Most commonly, statistical hypothesis tests assume that the population measurements are normally distributed (Exercise 4 highlights the specific reasoning for this).

While it is usually not possible to directly examine the distribution of measurements in the whole population to determine whether or not this requirement is satisfied or not (for the same reasons that it is not possible to directly measure population parameters such as population mean), if the sampling is adequate (unbiased and sufficiently replicated), the distribution of measurements in a sample should reflect the population distribution. That is a sample of measurements taken from a normally distributed population should be normally distributed.

Tests on data that do not meet the distributional requirements may not be reliable, and thus, it is essential that the distribution of data be examined routinely prior to any formal statistical analysis.

End of instructions

  EDA - Homogeneity of variances for regression

The assumption of homogeneity of variance is equally important for regression analysis and in particular, it is prospect of a relationship between the mean and variance of y-values across x-values that is of the greatest concern. Strictly the assumption is that the distribution of y values at each x value are equally varied and that there is no relationship between mean and variance. However, as we only have a single y-value for each x-value, it is difficult to determine whether the assumption of homogeneity of variance is likely to have been violated (mean of one value is meaningless and variability can't be assessed from a single value). The figure below depicts the ideal (and almost never realistic) situation in which there are multiple response variable (DV) observations for each of the levels of the predictor variable (IV). Boxplots are included that represent normality and variability.

Inferential statistics is based around repeatability and the likelihood of data re-occurrence. Consider the following scatterplot that has a regression line (linear smoother - line of best fit) fitted through the data (data points symbolized by letters).

Points that are close to the line (points A and B) of best fit (ie those points that are close to the predicted values) are likely to be highly repeatable (a repeat sampling effort is likely to yield a similar value). Conversely, points that are far from the line of best fit (such as points F and G) are likely to take on a larger variety of values.
The distance between a point (observed value) and the line of best fit (predicted value) is called a residual. A residual plot plots the each of the residuals against the expected y values. When there is a trend of increasing (or decreasing) spread of data along a regression line, the residuals will form a wedge shape pattern. Thus a wedge shape pattern in the residual plot suggests that the assumption of homogeneity of variance may have been violated.

Of course, it is also possible to assess the assumption of homogeneity of variance by simply viewing a scatterplot with a linear smoother (linear regression line) and determining whether there is a general increase or decrease in the distance that the values are from the line of best fit.

End of instructions

  Model I vs Model II Regression

Model I regression (fixed X regression)

The purpose of simple linear regression analysis is to estimate the slope and y-intercept of a straight line through a data set. The line represents the expected (and predicted) average values of X and Y in the population, based on the collected sample. The line (and thus the slope and intercept) is typically the line that minimizes the vertical spread of the observations from the line. This process of fitting the line of best fit is called Ordinary Least Squares (OLS), and is depicted in figure OLS Y vs X (top left) below. This fitting process assumes that there is no uncertainty in the predictor (X) variable and therefore that the observed values of X are exactly as they are in the population (there is no measurement error nor natural variation).

Model I regression is the classical regression analysis and the form of analysis most commonly used. However, it is only a valid method of estimating the model parameters (slope and intercept) when the levels of the predictor variable are not measured, but rather are set by the researcher. For example, if we were interested in the effects of temperature on the growth rate of plant seedlings, we could analyse the data using model I regression provided the different temperatures were specifically set by us (eg. controlling temperatures in green houses or growth cabinets). If on the other hand, the plants had been grown under a range of temperatures that were not specifically set by us and we had simply measured what the temperatures were, model I regression would not be appropriate.

Note that if instead of regressing Y against X we regressed X against Y, the slope of the line of best fit would be different since the line is now the one that minimizes the horizontal spread of the observations from the line (see figure OLS X vs Y - topright). The OLS regressions of Y on X and X on Y represent the two extremes of the population slope estimates as they depict the situations in which all of the variation is in the vertical and horizontal axes respectively. Typically, we might expect some uncertainty in both X and Y variables, and thus the true trend line should lie somewhere between these two extremes (see the bottom right figure below).


Model II regression (random X regression)

Model II regression estimates the line of best fit by incorporating uncertainty in both Y and X variables, and is therefore more suitable for estimating model parameters (slope and intercept) from data in which both variables have been measured. There are at least three forms of model II regression and these differ by what assumptions they place on the relative degree of uncertainty in Y and X variables

The bottom right figure depicts each of the regression lines through a data set. Note the following:
  1. All estimated lines pass through a central point. This point is the mean value of Y and the mean value of X. The different regression fitting procedures essentially just rotate the line of best fit (major axis) through the data set. They differ in the degree to which the major axis is rotated.
  2. That the OLS lines form the extreme estimated lines of best fit.
  3. The RMA line is exactly half way between the two OLS lines
  4. Since for this example, the Y and X variable were measured on substantially different scales (where the degree of uncertainty in X is far greater than the degree of uncertainty in Y), the MA regression fitting procedure is equivalent to OLS X vs Y (assumes all uncertainty is in X and non in Y)

Implications

Given that most instances of regression in biology are actually more suitable for model II regression, why are examples of model II in the literature so rare and why do most statistical software default to model I (OLS) regression procedures (most do not even offer model II procedures)? Is it that biologists are ignorant or slack? It turns out that as far as the main hypothesis of interest is concerned (that the population slope) equals zero, it does not matter - RMA and OLS procedures give the same p-values (p-values cant be easily computed for MA and Ranged MA procedures).

If the purpose of the regression is to generate a model that can be used for the purpose of prediction (predict new values of the dependent variable from new values of the independent values), then only OLS fitted models are valid. The reason for this, is that the new independent value represents a theoretical fixed value with no uncertainty. This new value must be used in a model that assumed no uncertainty in the independent (predictor) variable. The OLS procedure is the only one that minimizes the vertical spread of the observations from the line.

Therefore, if regression analysis is being performed for the purpose of investigating whether there is a relationship between two continuous variables and or to generate a predictive model, then model I (OLS) regression is perfectly valid. Note, however, that if slopes and intercepts are reported, it is probably worth presenting model I and model II slopes.

If on the other hand the nature of the relationship is important, and therefore it is important to get estimates of the slope and y-intercept that best represent the population relationship, then it is necessary to make the model II corrections. Good examples of where this is important are: As a final point, if the R2 value is very high, then estimated slopes will be very similar, irrespective of which line fitting procedure is used!


End of instructions

  R transformations

The following table illustrates the use of common data transmformation functions on a single numeric vector (old_var). In each case a new vector is created (new_var)

TransformationSyntax
loge

> new_var <- log(old_var)

log10

> new_var <- log10(old_var)

square root

> new_var <- sqrt(old_var)

arcsin

> new_var <- asin(sqrt(old_var))

scale (mean=0, unit variance)

> new_var <- scale(old_var)

where old_var is the name of the original variable that requires transformation and new_var is the name of the new variable (vector) that is to contain the transformed data. Note that the original vector (variable) is not altered.

End of instructions

  R2 value

The R2 value is the proportion of the total variability in the dependent variable that can be explained by its linear relationship with the independent variable, and thus a measure of the strength of the relationship. The R2 value ranges from 0 (very very low) to 1 (extremely tight relationship). The R2 value for the data represented in the following relationship would be 1 - that is all of the variation in DV can be explained by a change in IV.

The R2 value for the data represented in the next relationship however, would be substantially less than 1 - whilst some of the variation in DV can be explained by a change in IV, changes in IV alone does not account for all the changes in DV.


End of instructions

  R2 value

Essentially you need to reconstruct the linear equation (y=mx+c) that relates the dependent variable with the independent variable (including the estimated slope and y-intercept), substitute the new x value, and solve for y. Remember that if any transformations where used, then the transformation functions (eg log) need to be incorporated into the linear equation.

Along with calculating a predicted value, it is often useful to obtain 'prediction' or 'confidence' intervals around this prediction. Whilst the terms 'prediction' and 'confidence' are often thought of as synonymous, but there are important differences.
'Confidence' intervals (around a prediction) pertain to predicted future POPULATION means. That is, for a given X, if we were to collect a sample of observations, 95% of intervals of the stated size are likely to contain the mean of this sample.
'Prediction' intervals (around a prediction) pertain to predicted future single observations. For a given X, if we collect a single observation, 95% of intervals of the stated size are likely to contain this observation.

Prediction intervals are thus larger than confidence intervals. As we are typically interested in population trends, we are typically interested in 'confidence' intervals. It should be noted that technically, these confidence and prediction intervals assume that there is no uncertainty in the X (predictor) variable - an assumption that is rarely satisfied.

End of instructions

  Model II regression analysis

# make sure that the biology library is loaded
> library(biology)
# fit the model II regression
> summary(lm.II(log10(INDIV)~log10(AREA), data, type="RMA"))

where log10(INDIV) is the name of the dependent (response) variable, log10(AREA) is the name of the independent (predictor) variable, data is the name of the dataset and type="RMA" indicates the form of regression to fit. Other types possible are; "MA" and "OLS".

End of instructions

  Raw or transmformed data?

Generally it is better to plot original (untransformed) data in any graphical summaries. Firstly, this people to examine the results without having to make any mental back-transformations. Secondly, transformations are usually only performed so as to satisfy the assumptions of a statistical test. A graph is not a statistical test. Rather it is a summary, and as such has no such assumptions.

A good compromise it to plot the raw data on transformed axes. This enables the magnitude of values to be examined, and yet also reflects the nature of the statistical model fitted.

End of instructions

  Simple linear regression

Linear regression analysis explores the linear relationship between a continuous response variable (DV) and a single continuous predictor variable (IV). A line of best fit (one that minimizes the sum of squares deviations between the observed y values and the predicted y values at each x) is fitted to the data to estimate the linear model.

As plot a) shows, a slope of zero, would indicate no relationship – a increase in IV is not associated with a consistent change in DV.
Plot b) shows a positive relationship (positive slope) – an increase in IV is associated with an increase in DV.
Plot c) shows a negative relationship.

Testing whether the population slope (as estimated from the sample slope) is one way of evaluating the relationship. Regression analysis also determines how much of the total variability in the response variable can be explained by its linear relationship with IV, and how much remains unexplained.

The line of best fit (relating DV to IV) takes on the form of
y=mx + c
Response variable = (slope*predictor   variable) + y-intercept
If all points fall exactly on the line, then this model (right-hand part of equation) explains all of the variability in the response variable. That is, all variation in DV can be explained by differences in IV. Usually, however, the model does not explain all of the variability in the response variable (due to natural variation), some is left unexplained (referred to as error).

Therefore the linear model takes the form of;
Response variable = model + error.
A high proportion of variability explained relative to unexplained (error) is suggestive of a relationship between response and predictor variables.

For example, a mammalogist was investigating the effects of tooth wear on the amount of time free ranging koalas spend feeding per 24 h. Therefore, the amount of time spent feeding per 24 h was measured for a number of koalas that varied in their degree of tooth wear (ranging from unworn through to worn). Time spent feeding was the response variable and degree of tooth wear was the predictor variable.

End of instructions