The Types of Models

[01]
>>
The Types of Models
Lloyd Allison,
School of Computer Science and
Software Engineering,
Monash University,
Australia 3800.
|
[20+5]
[more (click)]
|
Abstract:
The specification of various kinds of statistical model
from machine learning and data mining
is examined formally using the type and class system of the
functional programming language Haskell as a meta-language.
Types and classes (in the programming sense) of models, and
operations on models, are defined; many are naturally polymorphic.
Convenient conversion functions map between
the classes of models and extend their range of usefulness.
The result is a kind of theory of programming with models,
not only of using them.
The ``theory'' can run as an executable Haskell program or
can throw light on the foundations of platforms for programming
with statistical models.
Presented at the
Second Hawaii International
Conference on Statistics and
Related Fields (HICS03),
Honolulu, 2003 June 5-8.
This
document can be found at
users.monash.edu.au/~lloyd/Seminars/2003-HICS/index.shtml
and includes hyper-links to other resources.
The Types of Models

<<
[02]
>>
The problem & questions
-
- What are the products of machine-learning research?
AI, data mining, computational statistics,...
-
- How [ do | could ] they behave?
-
- What can you do to them?
-
- How can two or more of them be combined?
-
-
- What are their types and classes?
-
-
c.f. S-Plus, R, Weka, etc..
Also see [rules].
The Types of Models

<<
[03]
>>
Inspiration
- Functional Programming
i.e. programming with functions
-
- lambda-calculus,
Lisp, ..., SML, and
Haskell-98
-
- high-order functions (e.g. map, fold, zip,... etc.)
-
- lazy-evaluation
(e.g. ints = 0 : (map ((+) 1) ints))
-
- polymorphic types
(e.g. map :: (t->u) -> [t] -> [u])
-
- automatic type-inference
-
- type-classes
-
- type checked & compiled (fast)
-
So, trying to create ``programming with (statistical) models''
here
(using Haskell-98) ...
The Types of Models

<<
[04]
>>
... programming with models.
Conclusion (i)
- we get:
-
- high-order (functions of) models
- e.g. estimate Classification-Tree parameterized by (estimate Leaf Model)
- e.g. Classification-Tree -> Regression-Tree
-
- polymorphic typed (& checked) models
- e.g. a Model of some Bounded Enum <data-space>
- e.g. FunctionModel of <in-space> to <op-space>
-
- classes of statistical model
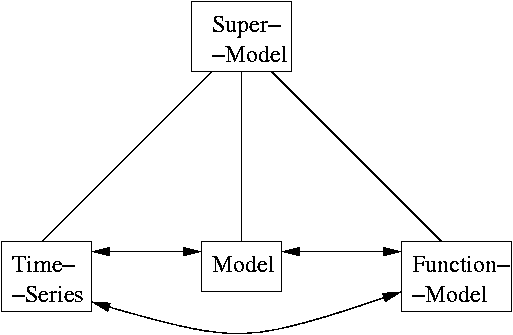
- e.g. (basic) Model, FunctionModel, TimeSeries, ¿other?
-
- (and lazy evaluation is useful in some algorithms)
NB. Some slight abuse of the type system.
The Types of Models

<<
[05]
>>
Example : (i) Mixture modelling
estMixture ests dataSet = let
...
... (22 lines of (E.M.) algorithm)
...
in mixture( ... .)
estMixture ::
- [ [dataSpace] -> [Float] -> Model of dataSpace ]
-- wtd estimators
- -> [ dataSpace ]
-- training data
- -> (Mixture) Model of dataSpace
unsupervised classification, clustering,
yes it works (slight abuse of types above).
NB. Mixture modelling chosen as an example `only'
because it is important in AI, ML, DM, CS.
Explain list [ ], function ->.
The Types of Models

<<
[06]
>>
Example : (ii) Classification- (decision-) Trees
estCTree estLeafMdl splits ipSet opSet = let
...
... (32 lines of code)
...
in ...
estCTree ::
- ( [opSpace] -> Model of opSpace )
-- leaf model est'
- -> ( ipSpace -> [ ipSpace -> Int ] )
-- partitioning
- -> [ipSpace] -> [opSpace]
-- training data
- -> CTree ipSpace opSpace
-- an instance of
FunctionModel ipSpace opSpace
-
- -- roughly (& it works),
types are inferred,
supervised classification,
tree chosen as `just' another standard AI example.
The Types of Models

<<
[07]
>>
turn a classification-tree into a FunctionModel- (regression-) tree
-
- ft = estCTree
(estFunctionModel2estModel
estLinearModel)
-- e.g.
- splits
- trainingIp trainingOp
-
-
- estFunctionModel2estModel
estFM
ipOpPairs =
- functionModel2model
(uncurry estFM (unzip ipOpPairs))
-
-
- and the types are inferred and checked.
-
-
- (E.g. Similarly, FunctionModel-mixtures, etc..)
The Types of Models

<<
[08]
>>
How (i) : (basic) Models
- The most important property of a (class of) statistical model
is ``pr'':
-
-
- class Model mdl where
-
- pr
:: (mdl dataSpace) -> dataSpace -> Probability
- msg2
:: (mdl dataSpace) -> dataSpace -> MessageLength
-- (data|model)
-
- msg :: . . .
(mdl dataSpace)
-> dataSpace
-> MessageLength
-- model + data|model
-
-
- -- a minimum; maybe[*] a Model
can also do other things.
([*] probably!)
Explain: must do something about over-fitting, use
minimum message length (MML: msg, msg2),
but could use any compositional criterion.
The Types of Models

<<
[09]
>>
example : a Model of non -ve Ints
| n | code2 | bits | cat'n | cum' cat'n |
|---|
| 0 | 0 | 1 | 1 | 1 |
| 1 | 100 | 3 | 1 | 2 |
| 2 | 10100 | 5 | 2 | 4 |
| 3 | 11000 | 5 |
| 4 | 1010100 | 7 | 5 | 9 |
| ... | ... | ... |
wallaceIntModel = -- 1 3 5 5 7 ...
let
catalans = -- 1 1 2 5 14 ...
let cats last n =
let next = last*2*(2*n-1) `div` n
in (next `div` (n+1)):(cats next (n+1))
in 1 : (cats 1 1)
cumulativeCatalans = scanl1 (+) catalans
in
MMsg 0 (\n -> (find n 0 cumulativeCatalans)*2+1)
Laziness useful.
MMsg a constructor of a type which is an instance of Model.
No parameters so msg length is zero.
The Types of Models

<<
[10]
>>
How (ii) : other classes of statistical models
- class FunctionModel fm where
-
- condModel
:: (fm inSpace opSpace) -> inSpace
-> ModelType opSpace
-
- condPr
:: (fm inSpace opSpace) -> inSpace
-> opSpace
-> Probability
-
- . . .
-
-
- class TimeSeries tsm where
-
- predictors
:: (tsm dataSpace) -> [dataSpace]
-> [ModelType dataSpace]
-
- prs
:: (tsm dataSpace) -> [dataSpace]
-> [Probability]
-
- . . .
(Also message lengths.)
E.g. regressions, linear regressions, and Markov models, etc..
One day even more classes.
The Types of Models

<<
[11]
>>
SuperModels
Our classes have some common properties;
we need a super-class. Obviously...
- class SuperModel sMdl where
- prior :: sMdl -> Probability
- mixture
:: (Mixture mx, SuperModel (mx sMdl)) =>
mx sMdl -> sMdl
- msg1 :: sMdl -> MessageLength
-
-
- class Mixture mx where
- mixer :: (SuperModel t) => mx t -> ModelType Int
- components :: (SuperModel t) => mx t -> [t]
-
-
- instance SuperModel (ModelType dataSpace) where
- msg1 (MPr mdlLen p) = mdlLen
- . . . etc.
The Types of Models

<<
[12]
>>
The Types of Models

<<
[13]
>>
Conversion functions ~ generality
e.g.
- functionModel2model fm ::
(FunctionModel fm) =>
- fm ipSpace opSpace
-> Model of (ipSpace, opSpace)
-
- &
-
- estFunctionModel2estModel ::
- ( ipSpace -> opSpace
-> FunctionModel of ipSpace opSpace )
-> ( [ (ipSpace, opSpace) ]
-> Model of (ipSpace, opSpace) )
-
(Also recall use with [tree]-models.)
(slight abuse of types)
The Types of Models

<<
[14]
>>
Rules of the game
(self imposed
-- recall [problem])
- Not:
- a library of heavy-weight machine learning algorithms,
- external subroutine calls
- a library of `interpreted' structures, or
- another special-purpose statistical language.
-
- Rather:
- use an existing language (Haskell-98)
- create a ``standard prelude'' of
models (c.f. Lists)
- so that estimators & models are
well-integrated with functions, lists, etc.,
- small building blocks,
e.g. bivariate, model2timeSeries, etc.,
- use the language's standard features --
- type-classes, polymorphic types, static type-checking,
high-order functions, lazy-evaluation, lists, etc.
because: want some sort of theory/ model/ semantics/ prelude
of models and modelling.
The Types of Models

<<
[15]
Conclusion (ii)
- (basic) Models
- e.g. univariate, multivariate, probability distributions
-
- FunctionModels
- e.g. regressions, classification trees, regression trees
-
- TimeSeries
- e.g. Markov models
-
- Mixtures of the above
-
- Conversion functions on classes of models and estimators.
-
- Polymorphic types, statically checked.
Also recall slide <04<.
- Allison, L., Powell, D., Dix, T. I.:
Compression and Approximate Matching,
Computer Journal 42(1) (1999) pp.1--10 (now generalized)
- Farr, G. E., Wallace, C. S.:
The Complexity of Strict Minimum Message Length Inference,
Computer Journal 45(3) (2002) pp.285--292
- Peyton Jones, S. {et al}:
Report on the Programming Language Haskell 98,
http://www.haskell.org/ (1999-2003), also,
Haskell98 Language and Libraries, the Revised Report,
Cambridge U.P. (2003)
- Wallace, C. S., Freeman, P. R.:
Estimation and Inference by Compact Coding,
Journal of the Royal Statistical Society series B.
49(3) (1987) pp.240--265
- Wallace, C. S., Patrick, J. D.: Coding Decision Trees.
Machine Learning 11 (1993) pp.7--22
6/2003 ©
L. Allison,
School of Computer Science and Software Engineering,
Monash University, Australia 3168.
Created with "vi (Linux & Solaris)", charset=iso-8859-1