On the diffusive propagation of warps in thin accretion discs

Giuseppe Lodato, Daniel J. Price
[ full text pdf (340 kb) ], accepted for publication in MNRAS 14/02/10 (arXiv:1002.2973).Abstract
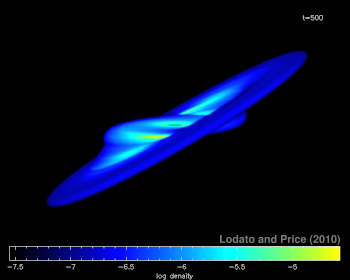
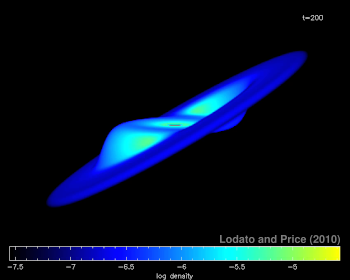
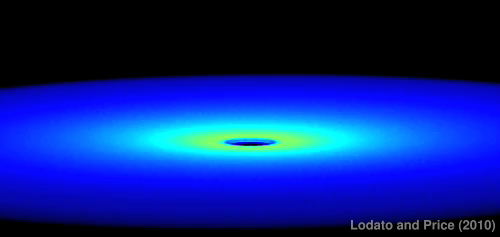
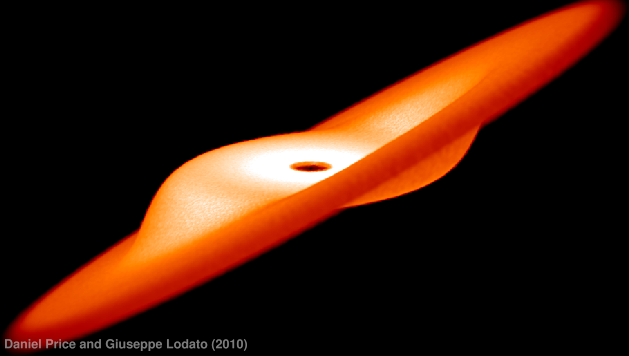
In this paper we revisit the issue of the propagation of warps in thin and viscous accretion discs. In this regime warps are know to propagate diffusively, with a diffusion coefficient approximately inversely proportional to the disc viscosity. Previous numerical investigations of this problem (Lodato & Pringle 2007) did not find a good agreement between the numerical results and the predictions of the analytic theories of warp propagation, both in the linear and in the non-linear case. Here, we take advantage of a new, low-memory and highly efficient Smoothed Particle Hydrodynamics (SPH) code to run a large set of very high resolution simulations (up to 20 million SPH particles) of warp propagation, implementing an isotropic disc viscosity in different ways, to investigate the origin of the discrepancy between the theory and the numerical results. We identify the cause of the discrepancy in an incorrect calibration of disc viscosity in Lodato & Pringle (2007). Our new and improved analysis now shows a remarkable agreement with the analytic theory both in the linear and in the non-linear regime, in terms of warp diffusion coefficient and precession rate. It is worth noting that the resulting diffusion coefficient is inversely proportional to the disc viscosity only for small amplitude warps and small values of the disc $\alpha$ coefficient ($\alpha\lesssim 0.1$). For non-linear warps, the diffusion coefficient is a function of both radius and time, and is significantly smaller than the standard value. Warped accretion discs are present in many contexts, from protostellar discs to accretion discs around supermassive black holes. In all such cases, the exact value of the warp diffusion coefficient may strongly affect the evolution of the system and therefore its careful evaluation is critical in order to correctly estimate the system dynamics.
Images | |

|

|

|

|

|

|

|

|
Images and movies were produced using SPLASH, a free visualisation tool for SPH data.