note on [prac 2], CSE2304, 4/2002

Note that the core (suggested) algorithms for problems A and B are essentially the same:

• suitable initialisation of boundary condition(s);
• for g from 1 to some_limit do
  • for j from g to n do
    • best_so_far := very_bad ;
    • for i from g-1 to j-1 do
      • x := combine( m[g-1,i], one(i+1, j) );
      • if x better than best_so_far then
        • best_so_far := x;
        • and remember associated details, e.g. i's value
    • m[g, j] := best_so_far ; and store associated details

We store partial results in m[,].   m[p,q] is a partial solution that is constrained to use exactly p [lines or segments] for q [words or data values].

The solutions [line-breaks or cut-points] can be found by tracing back from m[p,n], retracing backwards the choices made when computing the values in m[,] forward.

Another way to look at it

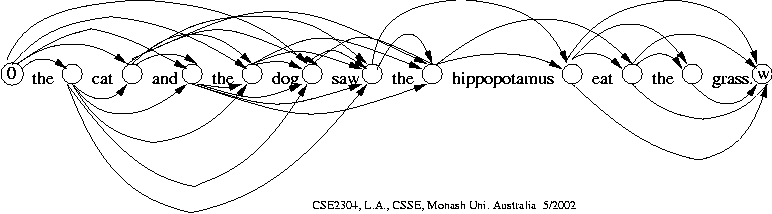
Create a weighted, directed [graph] (it's actually a DAG) with a vertex "in between" each word. The weight of an edge from the vertex before word i to the vertex after word j is the cost of a single line containing exactly the words i to j inclusive (if this is possible). Note that edges into v_w have zero cost (last line).

Find the [shortest path] from v₀ to v_w.

A similar observation can be made about graphs and the data segmentation problem (group B), but an edge "over" a single data value has weight zero, so that is what a shortest-path algorithm will use unless either (i) there is some penalty for using a path of many edges, or (ii) it is modified to force it to choose among paths of at most g edges.