Inductive programming (IP)
is about components for
It employs Haskell and MML.
Here IP is illustrated by a
Online at: users.monash.edu.au/~lloyd/Seminars/2006-ACSC/index.shtml 1/2006.
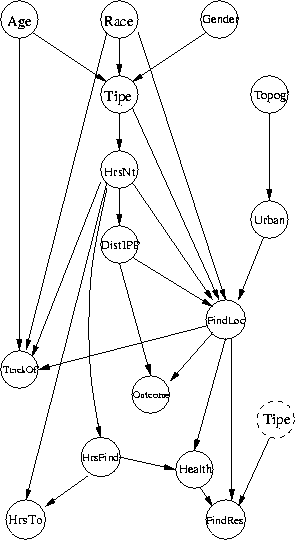
Some variable types...
@0: Tipe = Alzheimers | Child |... @1: Age @2: Race = ... @3: Gender = ... @4: Topography = as above @5: Urban = ... @6: HrsNt @7: DistIPP @8: TrackOffset @9: Health = Well | Hurt | Dead --after! @10: Outcome = Find | Suspended | Invalid @11: FindRes = Ground | Air |...| Dog @12: FindLoc = Brush | Woods |... @13: HrsFind @14: HrsTot
|
^ | | | | h | | | | | v | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Components must be autonomous or must cooperate,
For data D and model M,
| Bayes: |
pr(M&D)
|
| Shannon: | msgLen(E) = -log(pr(E)) |
| Wallace: |
msgLen(M&D)
|
| Receiver |
| Transmitter |
| <------------------ |
(NB. MML is not in general identical to MAP,
estNetwork perm estMV dataSet =
let
n = (length . selAll) (estMV [])
search _ [] = [] --done
search ps (c:cs) =
--parents ps, children c:cs
let
opFlag = ints2flags [c] n --child
ipFlags = ints2flags ps n --parents
cTree = estCTree --see JFP 2005
(estAndSelect estMV opFlag)
(splitSelect ipFlags)
dataSet dataSet
in cTree : (search (c:ps) cs)
trees = search [] perm --network
msgLen = sum (map msg1 trees) --total msg1
nlP datum = sum (map(\t -> condNlPr t datum datum) trees)
in
MnlPr msgLen nlP --return a Model
(\() -> "Net:"++(show trees))
class Project t where --as in a Projection type
select :: [Bool] -> t -> t
...
Lets us select certain variables (columns), e.g.
data ModelMV dataSpace = MnlPrMV... --new Model type ... instance Model ModelMV where ... instance Project (ModelMV dataSpace) where ...
class Splits2 ds where
splitSelect :: [Bool]->[ds]->[Splitter ds]
modelMaybe m1 m2 =
let
negLogPr (Just x) = nlPr m1 True + nlPr m2 x
negLogPr Nothing = nlPr m1 False
in
MnlPr (msg1 m1 + msg1 m2) negLogPr
...'show' method omitted
-- a useful inductive programming (IP) operator,
estModelMaybe estModel dataSet =
let
present (Just _) = True
present Nothing = False
m1 = uniformModelOfBool --[*]
m2 = estModel (map (\(Just x)->x)
(filter present dataSet))
in modelMaybe m1 m
(This is not the same as coding missing as a 'special value'.)
[*] Or alternatively...
m1 = estMultiState (map present dataSet)or even...
m1 = commonKnowledge¿Do you want to model 'missingness', or not?
data Tipe = Alzheimers| Child| Despondent| ...
type Age = Double
...
data Topography = Mountains| Piedmont| Tidewater
deriving (Ord, Enum, Bounded,...)
...
type MissingPerson = (Maybe Tipe, Maybe Age, ... )
--standard Haskell-98.
e0 = estModelMaybe estMultiState --Tipe
e1 = estModelMaybe(estNormal 0 90 1 70 0.5) --Age
... etc.
estMissingPerson = estVariate15 e0 e1 e2 e3 e4 e5 e6
e7 e8 e9 e10 e11 e12 e13 e14
...
instance Splits Topography where splits = splitsBE
--or alternatively = splitsOrd
... etc.
splitsBE --for Bounded Enum types,
splitsOrd --for Ord types
Also implemented 'setSplits' for high-arity Bounded Enum types.
dataSet = read (readFile theDataFile)
:: [MissingPerson] --input
nw = estNetwork [1,2,3,0,4,5,6,7]
estMissingPerson dataSet --model
nullModel = estMissingPerson dataSet --null