Modelling discontinuities and Kelvin-Helmholtz instabilities in SPH
Daniel J. Price
[ high resolution pdf (2.6Mb) ] accepted to J. Comp Phys on 07/08/08 [ low res version at arXiv:0709.2772 ]Abstract
In this paper we discuss the treatment of discontinuities in Smoothed Particle Hydrodynamics (SPH) simulations. In particular we discuss the difference between integral and differential representations of the fluid equations in an SPH context and how this relates to the formulation of dissipative terms for the capture of shocks and other discontinuities.
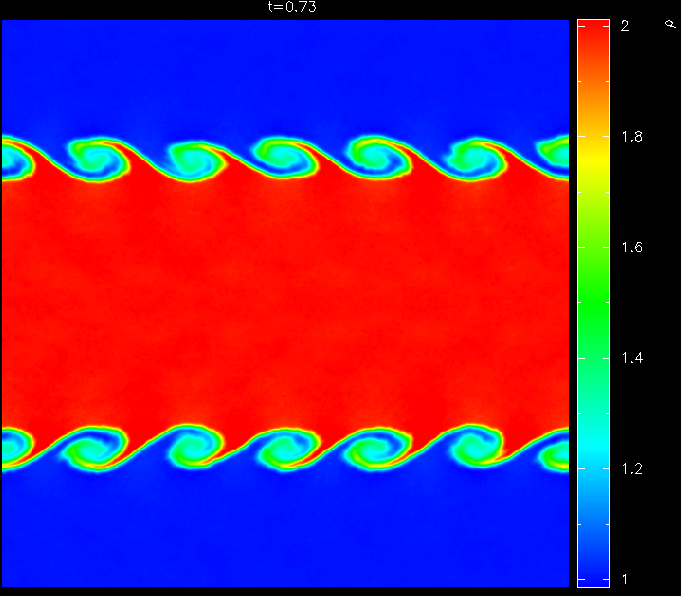
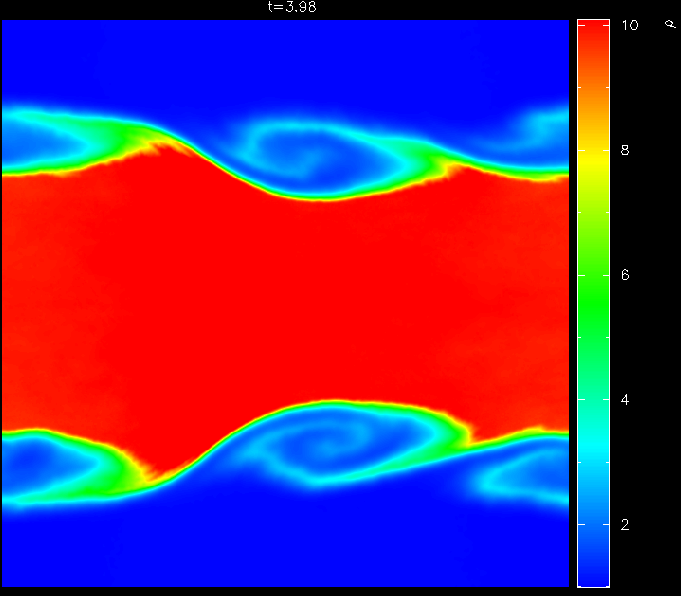
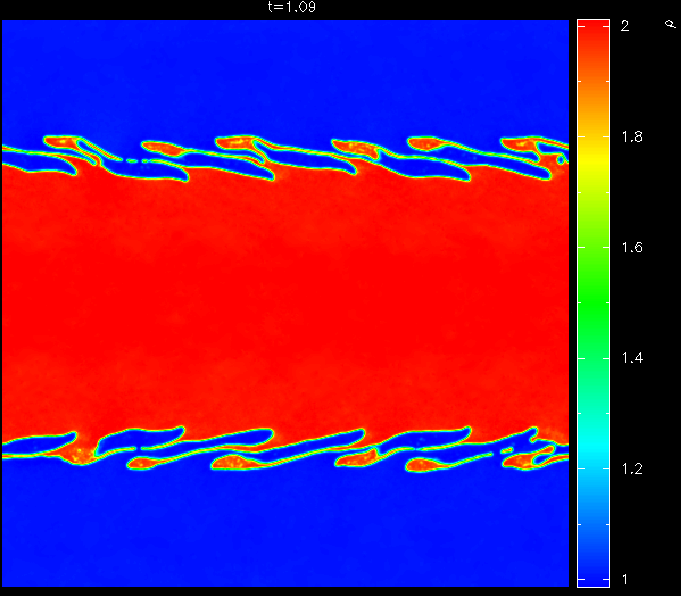
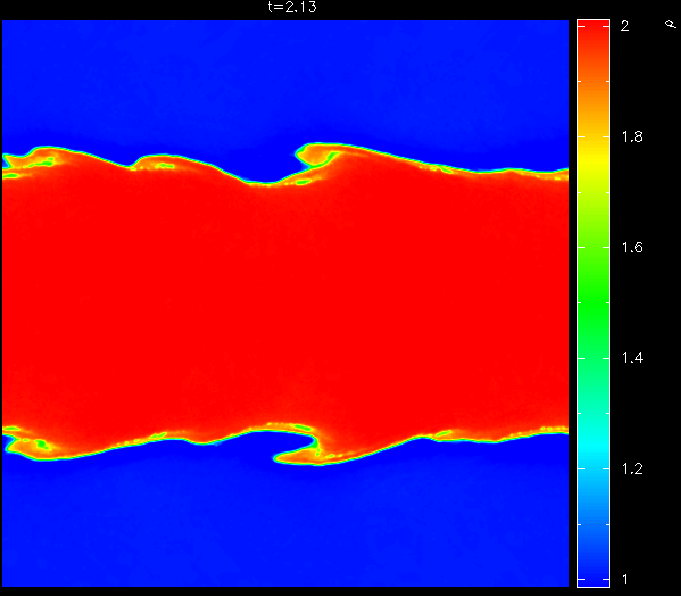
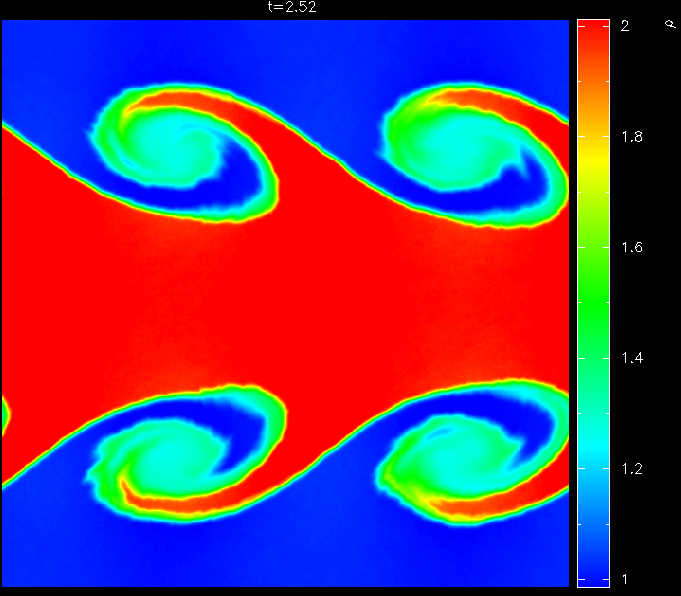
This has important implications for many problems, in particular related to recently highlighted problems related to treating Kelvin-Helmholtz instabilities across contact discontinuities in SPH. We highlight in this paper that the ``fundamental differences'' between SPH and grid based methods suggested by Agertz et al. are actually more like ``fundamental similarities'' relating to the fact that both types of method require an appropriate treatment of all flow discontinuities.
The specific problems pointed out by Agertz et al. are shown to be related in particular to the treatment of contact discontinuities in SPH which can be cured by the simple application of an artificial thermal conductivity term. We propose a new formulation of artificial thermal conductivity in SPH which minimises dissipation away from discontinuities and can therefore be applied quite generally in SPH calculations.