Guillaume Laibe
Dust evolution in protoplanetary discs
A new SPH gas and dust algorithm to simulate star and planet formation
Collaborators: Dr. D.J. Price (Monash University, Melbourne), Dr. B.A. Ayliffe (Monash University, Melbourne) and Prof. M.R. Bate (University of Exeter, UK).
To study the influence of dust and ambipolar diffusion on star formation, I have developed a general multifluid algorithm which is implemented in the world-class SPH code PHANTOM of Dr. D.J. Price to give an accurate treatment of the multifluid magnetohydrodynamics. Specifically, my goal is to treat simultaneously ambipolar diffusion and the evolution (dynamics and growth) of the dust grains. The numerical tool achieved will be the first one able to deal consistently with a broad range of problems related to star and planet formation.
The interactions between the different phases of a multifluid flow depend essentially on the drag force between each phase. Star and planet formation problems require an efficient treatment of the strong drag regimes (where the drag stopping times are much smaller than the courant time; small grains and ambipolar diffusion), as well as large friction timescales (large grains and planetesimals) with a benchmarked accuracy. I have therefore developed a new versatile multifluid and highly performing algorithm, suitable for every astrophysical drag regime.
The fundamental properties of this algorithm are:
- An accuracy improved by a factor ~10-100 for the same computational cost compared to the old formalisms, where this improvement comes from a new SPH interpolation for multifluid flows.
- The exact conservation of energy, linear and angular momentum inherent in the SPH method.
- An exhaustive treatment of all the astrophysical drag regimes, linear and non-linear (absolutely necessary to treat the evolution of pre-planetesimals correctly).
- The Lagrangian treatment of the dust dynamics, enables backtracking of the particles history, avoiding the inherent difficulties of such a process in Eulerian methods.
- An efficient implicit treatment of the strong drag regimes which avoids (1) the prohibitive computational costs related to small timesteps and (2) the problem of numerical over-dissipation due to a lack of spatial resolution in every existing gas and dust code. This property in necessary to study the evolution of micron sized grains constrained by the observations (this stage is nearly finalised).
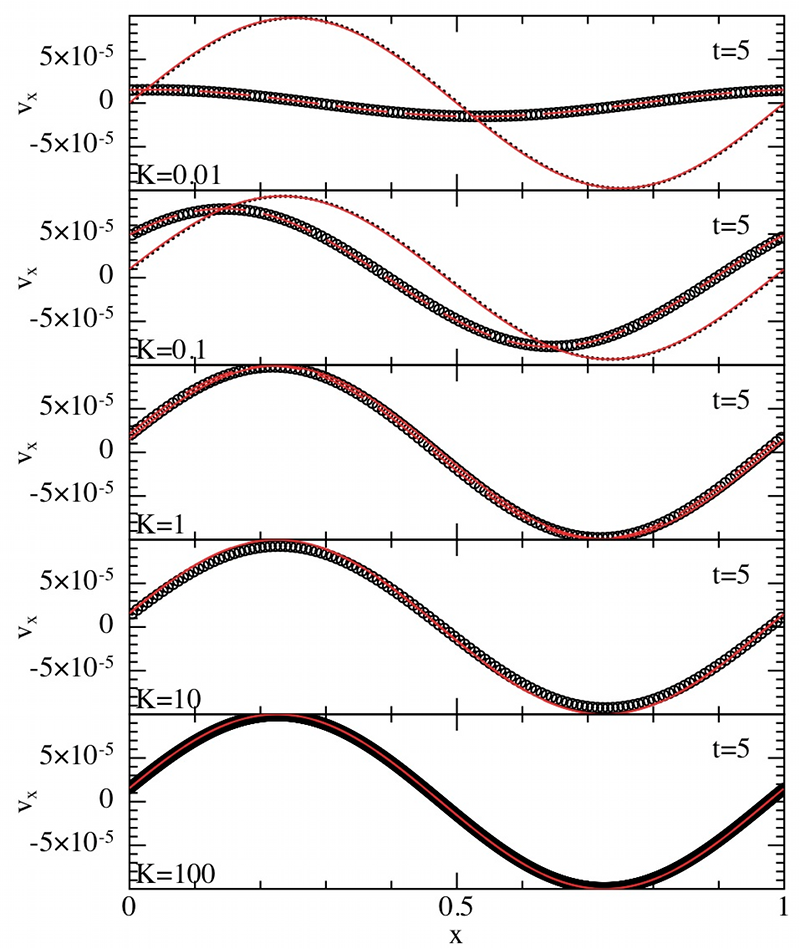
This phase of development from scratch represents 18 months of work. Its achievement culminated in three publications specific to the gas and dust interactions in MNRAS (Laibe and Price 2011, 2012a and b). The reliability of the algorithm has been proven by performing the most exhaustive benchmarking test series for gas and dust codes to date (Figure 3). Several issues addressed in this development are not specific to the SPH method and are also important in any code doing gas and dust mixtures (particularly the spatial resolution criterion for strong drag regimes and the need to over resolve the gas compared to the dust).
A first application to planet formation has been obtained with the preliminary version of the algorithm in collaboration with Dr. B.A. Ayliffe and Pr. M.R. Bate (Ayliffe et al. 2012). Favourable locations for satellites and secondary planets (gaps in the disc, mean-motion resonances) were systematically studied for a broad range of masses of the main planet in the disc. I am currently working on using the algorithm on several aspects of planet formation: SPH simulations of streaming instability and ambipolar diffusion, evolution of dust in multi-bodies systems and planning to study dusty turbulence as well.
The development of this SPH algorithm raised also important issues on the theory of SPH kernels. Thus, I conducted a theoretical analysis of the analysis of the SPH errors. From this, we set up in collaboration with Dr. D.J. Price a practical guide to convergence in Smoothed Particle Hydrodynamics (Laibe and Price 2013 in prep.).
