Navigation

Analytic model for dust evolution in discs

Collaborators: Dr. J.-F. Gonzalez (CRAL, Lyon) and A.Pr. S.T. Maddison (Swinburne University, Melbourne), Dr. C. Pinte (IPAG, Grenoble).

Figure2
Figure 2: Evolution of the dust scale heighth with growing grains for different values of the correlation time teddy of the turbulence. The plot highlights a brutal bifurcation for a critical value of Ωkteddy ~5. For small values of the typical turbulent correlation time teddy the dust layer behaves as it was found for diffusive processes. However, at larger correlation times, the dust layer collapses to an infinitely thin sheet in a short finite time.

The seminal theory of the radial-drift barrier (Weidenschilling 1977; Nakagawa et al. 1986) predicts that grains which are millimetre/centimetre in size migrate quickly through a protoplanetary disc, and are accreted onto the central star. This process is a major theoretical obstacle to the formation of planet embryos as it depletes the reservoir of solid material. To explain how small grains survive the fast migration phase, I have derived an analytic work which revisits this theory. The underlying idea is that for realistic surface density and temperature profiles of discs, the gas drag and the acceleration due to the pressure gradient of the gas act in competition which varies as grains migrate and grow. This study culminated in 2012 with the submission/publication of five papers of which I am the first author: one published in A&A (Laibe et al. 2012), one submitted at A&A (in rev.) and three submitted to MNRAS.

I first derived analytic criteria for the simplest case of non growing grains. The outcome of the radial motion of non growing grains depend on the disc's surface density p and temperature q exponents (-p+q+1/2<0 for the Epstein regime and q<2/3 for larger bodies in the Stokes regime). Then, I computed with the radiative transfer code MCFOST the relation between p and q for a large set of disc's parameters to predict the grains behaviour in real discs. Finally, I derived another criterion (q<1) in an extensive study that includes grain growth. With this model, I retrieved all the properties exhibited by the dust grains in my numerical simulations. In particular, I explain quantitatively how the radial dependency of growth models (that strongly depends on the model of dusty turbulence) strongly helps grains for not being accreted onto the central star.

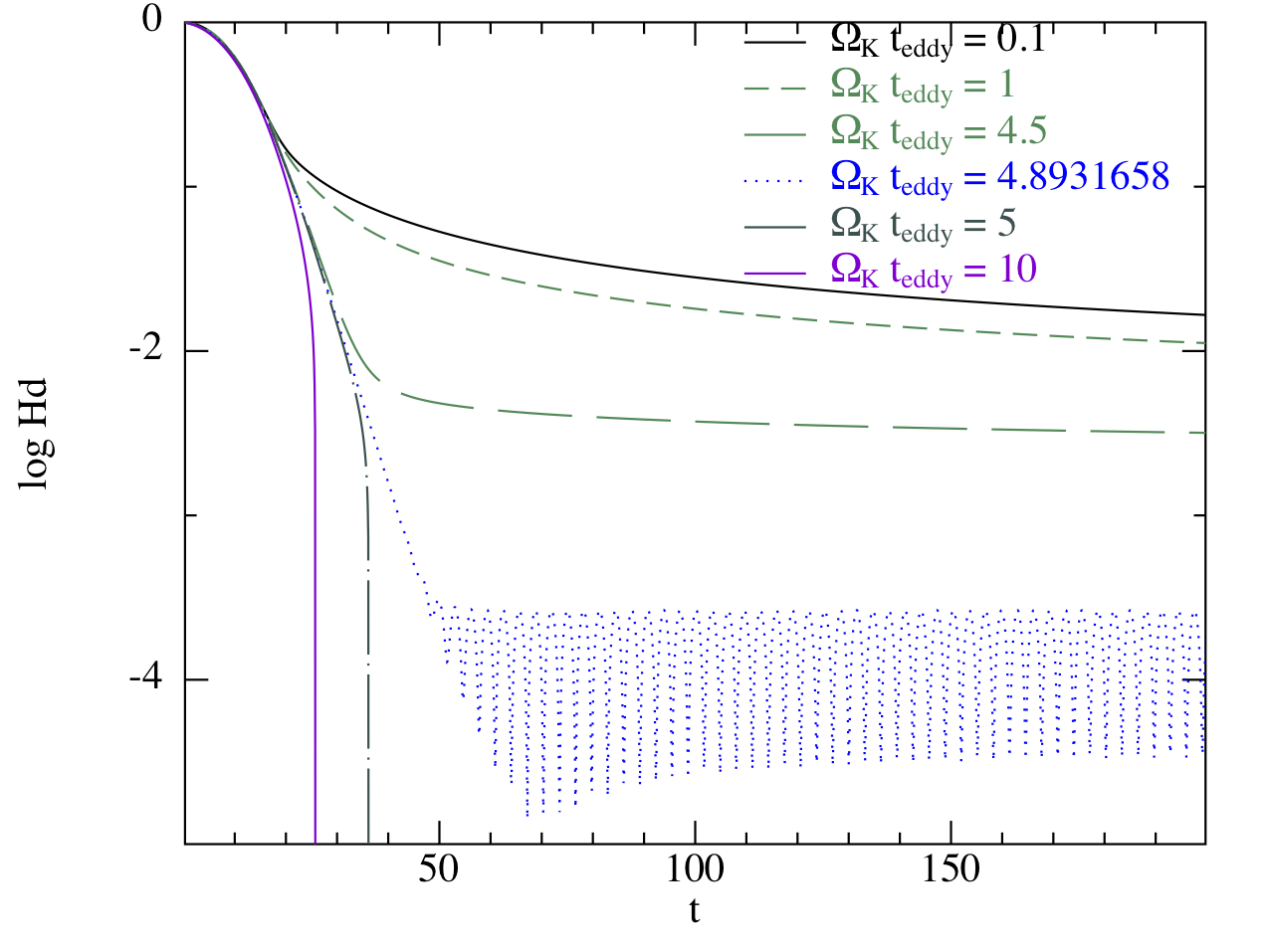
I also revisited analytically the theory of grains settling in discs, treating simultaneously the effects of grain growth and strirring by a correlated turbulence. I show that if the correlation time of turbulence is ~3-5 time the disc orbital period, grains efficicently collapse in the disc midplane (Figure 2), leading to a potential formation of planetesimal by gravitational collapse (the Goldreich-Ward mechanism).