What makes problems hard to optimise?
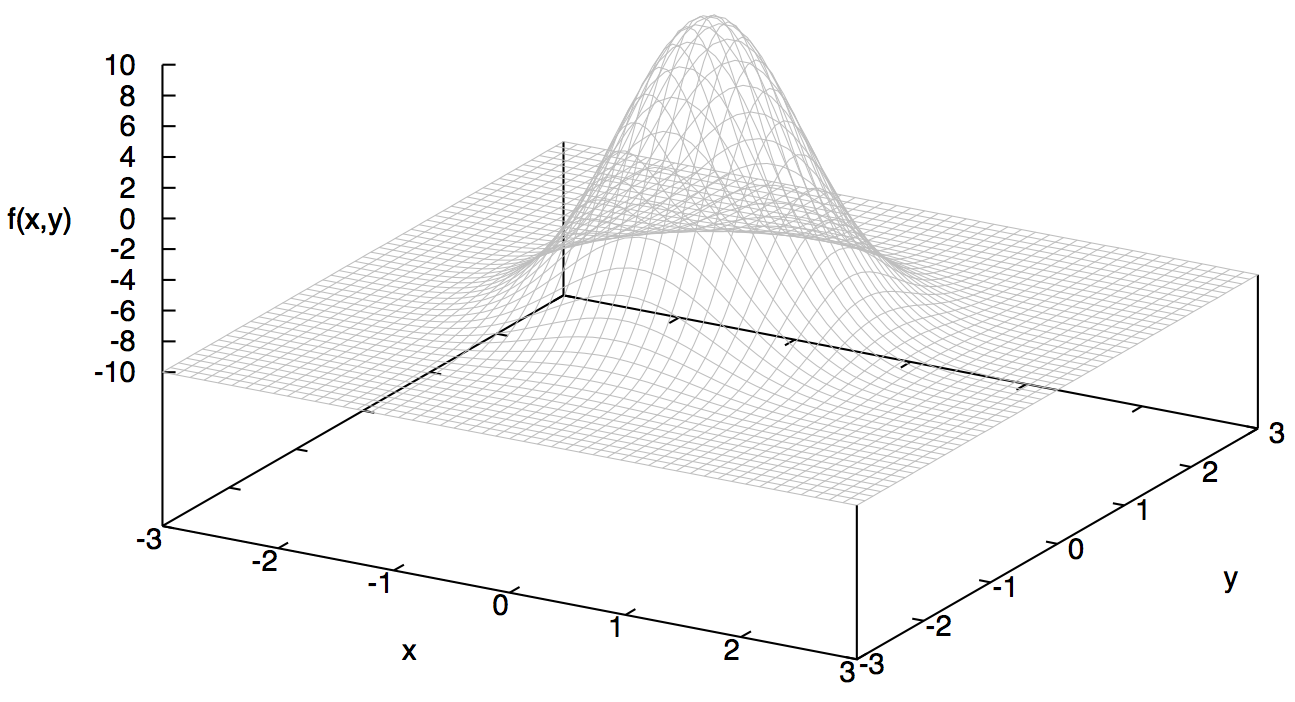
The topology of a fitness landscape is composed of certain features, such as local optima, global optimum and plateaus. A fitness landscape with one local optimum that is also the global optimum would be easy to search with a local search method. An example of a smooth fitness landscape is shown in the figure below.
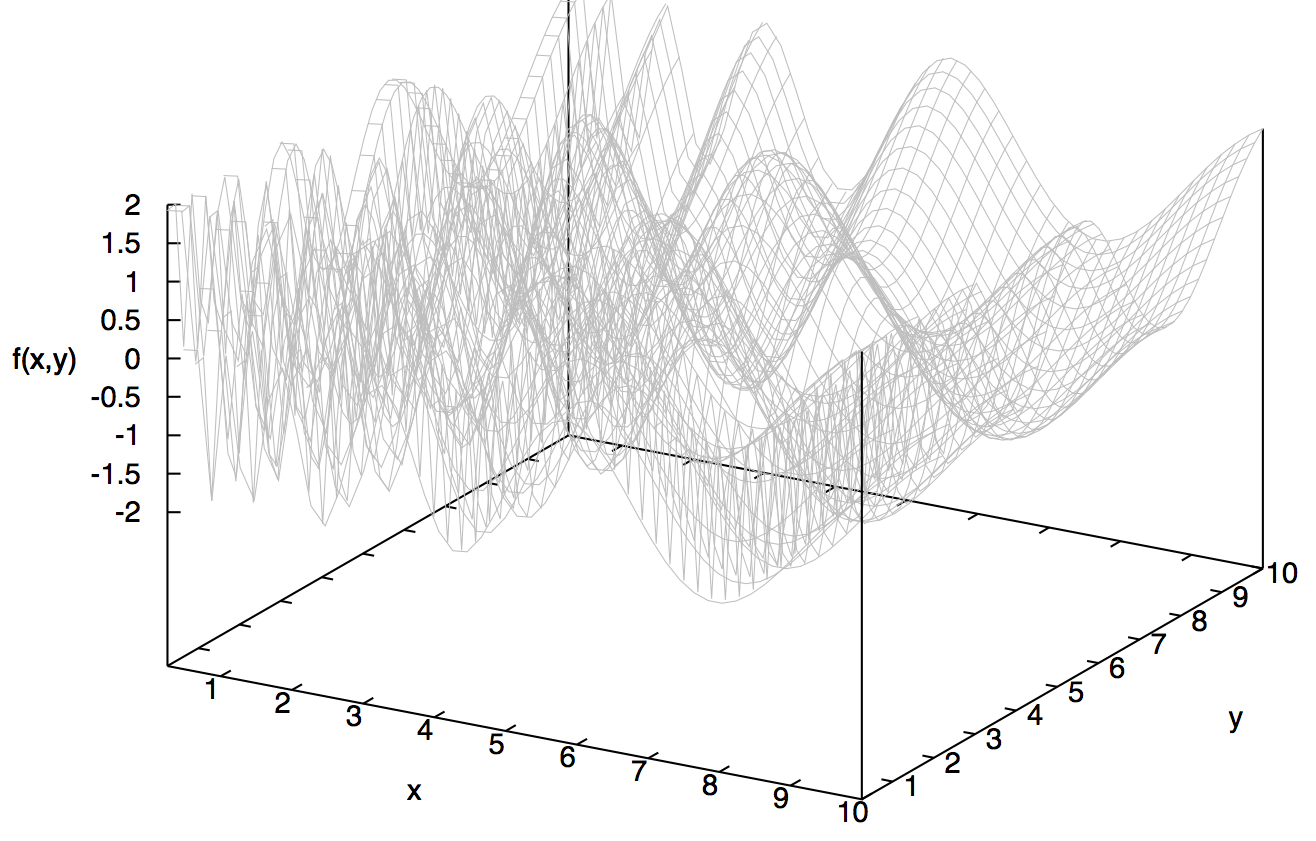
On the other hand, the existence of many local optima and an isolated global optimum makes the fitness landscape rugged and hard to explore, as the example shown below.
The choice of neighbourhood structure and the fitness function determine whether the fitness landscape is easy to search. For example, if the fitness difference between any two neighbouring solutions is on average small then the landscape is more likely to be suited for a wide range of local search operators. In contrast, if significant fitness difference is encountered in the neighbourhood, different operators will produce different quality results and the choice of the operator becomes important. In general, the concept of fitness landscape allows the study of the dynamics of the evolution of solutions, the comparative effectiveness of search methods and the ability of the algorithms to find good solutions to a given problem.